41 | 线性回归(下):如何使用最小二乘法进行效果验证?
黄申

该思维导图由 AI 生成,仅供参考
你好,我是黄申。
上一节我们已经解释了最小二乘法的核心思想和具体推导过程。今天我们就用实际的数据操练一下,这样你的印象就会更加深刻。我会使用几个具体的例子,演示一下如何使用最小二乘法的结论,通过观测到的自变量和因变量值,来推算系数,并使用这个系数来进行新的预测。
基于最小二乘法的求解
假想我们手头上有一个数据集,里面有 3 条数据记录。每条数据记录有 2 维特征,也就是 2 个自变量,和 1 个因变量。
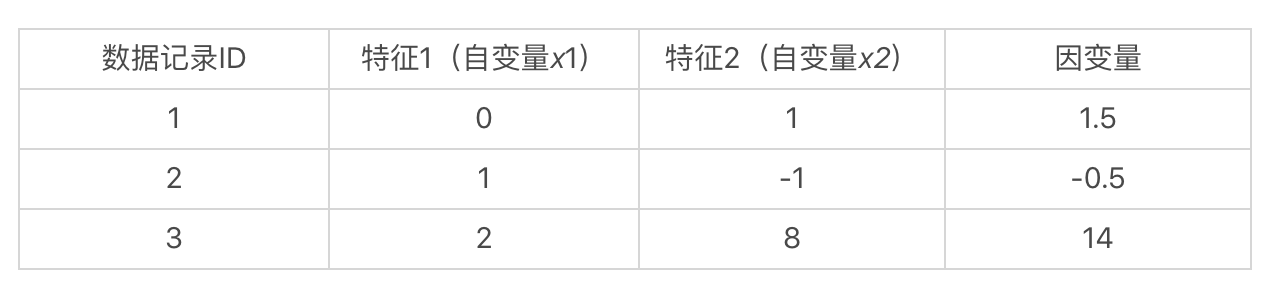
如果我们假设这些自变量和因变量都是线性的关系,那么我们就可以使用如下这种线性方程,来表示数据集中的样本:
也就是说,我们通过观察数据已知了自变量 、 和因变量 的值,而要求解的是 和 这两个系数。如果我们能求出 和 ,那么在处理新数据的时候,就能根据新的自变量 和 的取值,来预测 的值。
公开
同步至部落
取消
完成
0/2000
笔记
复制
AI
- 深入了解
- 翻译
- 解释
- 总结

本文介绍了线性回归模型的基本原理和最小二乘法的实现过程。通过详细的数学推导和Python代码示例,读者可以快速了解如何使用最小二乘法来计算线性回归模型的系数矩阵,并与sklearn库中的线性回归结果进行对比。文章还提到了线性回归模型的前提假设,以及如何使用决定系数R2来判断数据集是否适合使用线性模型。此外,文章还涉及到最小二乘法在非线性回归中的应用,以及提出了一个思考题供读者练习。通过本文的阅读,读者可以深入理解最小二乘法在线性回归中的应用,以及其在非线性回归中的潜在价值。
仅可试看部分内容,如需阅读全部内容,请付费购买文章所属专栏
《程序员的数学基础课》,新⼈⾸单¥68
《程序员的数学基础课》,新⼈⾸单¥68
立即购买
© 版权归极客邦科技所有,未经许可不得传播售卖。 页面已增加防盗追踪,如有侵权极客邦将依法追究其法律责任。
登录 后留言
全部留言(12)
- 最新
- 精选
 Joe回答与疑问: 1. 非线性关系的数据拟合,可以先将自变量转为非线性。如转化为多项式(sklearn的PolynomialFeatures)。再用线性回归的方法去拟合。 2. 请问老师对于求解逆矩阵有没有什么高效的方法? 附上以前写的polyfit方法,请老师指点。谢谢 def oneDPolynomiaTransform(self, x_origin): ''' @description: generate polynomial for 1D input data. rule: [x0, x0^2, x0^3,...,x0^degreee] @param {type} x_origin- data before transformed[nX1] @return: x_transformed- data after transformed[nXdegree] ''' len_features = len(x_origin) # polynomial feature data after transformed. x_transformed = np.array([]) for i in range(len_features): for j in range(self.degree+1): x_transformed = np.append( x_transformed, [(x_origin[i])**(j)]) x_transformed = x_transformed.reshape(-1, self.degree+1) return x_transformed
Joe回答与疑问: 1. 非线性关系的数据拟合,可以先将自变量转为非线性。如转化为多项式(sklearn的PolynomialFeatures)。再用线性回归的方法去拟合。 2. 请问老师对于求解逆矩阵有没有什么高效的方法? 附上以前写的polyfit方法,请老师指点。谢谢 def oneDPolynomiaTransform(self, x_origin): ''' @description: generate polynomial for 1D input data. rule: [x0, x0^2, x0^3,...,x0^degreee] @param {type} x_origin- data before transformed[nX1] @return: x_transformed- data after transformed[nXdegree] ''' len_features = len(x_origin) # polynomial feature data after transformed. x_transformed = np.array([]) for i in range(len_features): for j in range(self.degree+1): x_transformed = np.append( x_transformed, [(x_origin[i])**(j)]) x_transformed = x_transformed.reshape(-1, self.degree+1) return x_transformed作者回复: 写得很好,至于逆矩阵更好的求法,我要查一下资料看看有无更优的解。
2019-03-214 骑行的掌柜J感谢黄老师 之前一直只知道建模,拟合,预测,但是背后的数学原理一直没有很理解!!!现在有种恍然大悟的感觉!原来是这样,当因变量和自变量呈现线性关系,建模这一系列动作都是基于上面线代的原理!😁终于get到了它在求什么了!! PS:刚刚评论有个朋友也提问了如何判断一个数据集可以用线性模型?可以用R2,也就是regression.score这个方法, 所以请问黄老师:是只有先去用线性模型拟合数据集,再来判断模型是否合适吗? 还是我可以从拿到数据集一开始,直接查看每个自变量和因变量的关系是否呈线性再来决定线性模型是否合适?谢谢
骑行的掌柜J感谢黄老师 之前一直只知道建模,拟合,预测,但是背后的数学原理一直没有很理解!!!现在有种恍然大悟的感觉!原来是这样,当因变量和自变量呈现线性关系,建模这一系列动作都是基于上面线代的原理!😁终于get到了它在求什么了!! PS:刚刚评论有个朋友也提问了如何判断一个数据集可以用线性模型?可以用R2,也就是regression.score这个方法, 所以请问黄老师:是只有先去用线性模型拟合数据集,再来判断模型是否合适吗? 还是我可以从拿到数据集一开始,直接查看每个自变量和因变量的关系是否呈线性再来决定线性模型是否合适?谢谢作者回复: 你可以这么想象,如果只看一维变量,那么就是在二维平面上数据分布是不是像一根直线,而同时看多个变量,其实就是在多维空间中看数据分布是不是像一根直线,所以两者并不一样。如果在多维空间中有一条比较好的直线拟合,投影到单维空间,就不一定能很好的拟合了。
2020-07-033 叮当猫文中有提到,如何判断一个数据集是否可以用线性模型来表示,可以使用决定系数R2,随着自变量个数不断增加,R2将不断增大,这时需要用Rc2,而其中R2就是regression.score,那请问Rc2是库里面的什么呢?
叮当猫文中有提到,如何判断一个数据集是否可以用线性模型来表示,可以使用决定系数R2,随着自变量个数不断增加,R2将不断增大,这时需要用Rc2,而其中R2就是regression.score,那请问Rc2是库里面的什么呢?作者回复: 这是个好问题,我查了sklearn.linear_mode好像不提供这个数据。 你可以尝试一下statsmodels.api.OLS这个包,里面应该可以返回rsquared_adj
2019-04-172 Cest la vie老师好! 后面可以来一节PLS偏最小二乘的原理讲解和应用么
Cest la vie老师好! 后面可以来一节PLS偏最小二乘的原理讲解和应用么作者回复: 可以考虑到后面加餐的时候来一篇
2019-03-252
 罗耀龙@坐忘
罗耀龙@坐忘 茶艺师学编程 因为还不会编程,我只能用手算了…… B=[1.463916 -0.403059 -0.616992] 然后再算了误差,23.907,嗯,我有98%的信心相信我这次算错了。 而且我还不知道在哪里找错。 我想到如果是我在编写程序时出现这状况,很有可能会比这更惨……2020-05-064
茶艺师学编程 因为还不会编程,我只能用手算了…… B=[1.463916 -0.403059 -0.616992] 然后再算了误差,23.907,嗯,我有98%的信心相信我这次算错了。 而且我还不知道在哪里找错。 我想到如果是我在编写程序时出现这状况,很有可能会比这更惨……2020-05-064 余泽锋
余泽锋 import numpy as np X = np.mat([[1, 3, -7], [2, 5, 4], [-3, -7, -2], [1, 4, -12]]) Y = np.mat([[-7.5], [5.2], [-7.5], [-15]]) B1 = X.transpose().dot(X).I B2 = B1.dot(X.transpose()) B = B2.dot(Y) ''' matrix([[12.01208791], [-4.35934066], [ 0.82527473]]) '''2019-04-244
import numpy as np X = np.mat([[1, 3, -7], [2, 5, 4], [-3, -7, -2], [1, 4, -12]]) Y = np.mat([[-7.5], [5.2], [-7.5], [-15]]) B1 = X.transpose().dot(X).I B2 = B1.dot(X.transpose()) B = B2.dot(Y) ''' matrix([[12.01208791], [-4.35934066], [ 0.82527473]]) '''2019-04-244- Paul Shan高斯消元求得是精确解。 线性回归求得是最好近似解,覆盖高斯消元能处理的情况,也能在没有精确解的时候找到近似解,还提供测量近似参数,是处理线性关系的利器。2019-10-041
 qinggeouye""" 思考题同理 """ x = np.mat([[1, 3, -7], [2, 5, 4], [-3, -7, -2], [1, 4, -12]]) y = np.mat([[-7.5], [5.2], [-7.5], [-15]]) print("\n 系数矩阵 B: \n", (x.transpose().dot(x)).I.dot(x.transpose()).dot(y)) 系数矩阵 B: [[12.01208791] [-4.35934066] [ 0.82527473]]2019-03-301
qinggeouye""" 思考题同理 """ x = np.mat([[1, 3, -7], [2, 5, 4], [-3, -7, -2], [1, 4, -12]]) y = np.mat([[-7.5], [5.2], [-7.5], [-15]]) print("\n 系数矩阵 B: \n", (x.transpose().dot(x)).I.dot(x.transpose()).dot(y)) 系数矩阵 B: [[12.01208791] [-4.35934066] [ 0.82527473]]2019-03-301- 013923学习了!2022-09-15归属地:上海
 建强根据最小二乘法系数计算模型,用了一个简单的Python程序计算系数矩阵,程序代码: import numpy as np # 矩阵X X = np.array([[1, 3, -7] ,[2, 5, 4] ,[-3, -7, -2] ,[1, 4, -12] ] ) # X的转置X' TRANS_X = X.T # 目标值向量Y Y = np.array([[-7.5, 5.2, -7.5, -15]]).T # X'X B = TRANS_X.dot(X) # (X'X)^-1 B = np.matrix(B).I # [(X'X)^-1]X' B = B.dot(TRANS_X) # [(XX')^-1]X'Y B = B.dot(Y) print('系数矩阵:') print(B) print('验证:') print(X.dot(B)) ================程序输出结果================== 系数矩阵: [[12.01208791] [-4.35934066] [ 0.82527473]] 验证: [[ -6.84285714] [ 5.52857143] [ -7.17142857] [-15.32857143]]2020-10-25
建强根据最小二乘法系数计算模型,用了一个简单的Python程序计算系数矩阵,程序代码: import numpy as np # 矩阵X X = np.array([[1, 3, -7] ,[2, 5, 4] ,[-3, -7, -2] ,[1, 4, -12] ] ) # X的转置X' TRANS_X = X.T # 目标值向量Y Y = np.array([[-7.5, 5.2, -7.5, -15]]).T # X'X B = TRANS_X.dot(X) # (X'X)^-1 B = np.matrix(B).I # [(X'X)^-1]X' B = B.dot(TRANS_X) # [(XX')^-1]X'Y B = B.dot(Y) print('系数矩阵:') print(B) print('验证:') print(X.dot(B)) ================程序输出结果================== 系数矩阵: [[12.01208791] [-4.35934066] [ 0.82527473]] 验证: [[ -6.84285714] [ 5.52857143] [ -7.17142857] [-15.32857143]]2020-10-25
收起评论

