30 | 统计意义（上）：如何通过显著性检验，判断你的A/B测试结果是不是巧合？
黄申
该思维导图由 AI 生成，仅供参考
你好，我是黄申，今天我们来聊聊统计意义和显著性检验。
之前我们已经讨论了几种不同的机器学习算法，包括朴素贝叶斯分类、概率语言模型、决策树等等。不同的方法和算法会产生不同的效果。在很多实际应用中，我们希望能够量化这种效果，并依据相关的数据进行决策。
为了使这种量化尽可能准确、客观，现在的互联网公司通常是根据用户的在线行为来评估算法，并比较同类算法的表现，以此来选择相应的算法。在线测试有一个很大的挑战，那就是如何排除非测试因素的干扰。
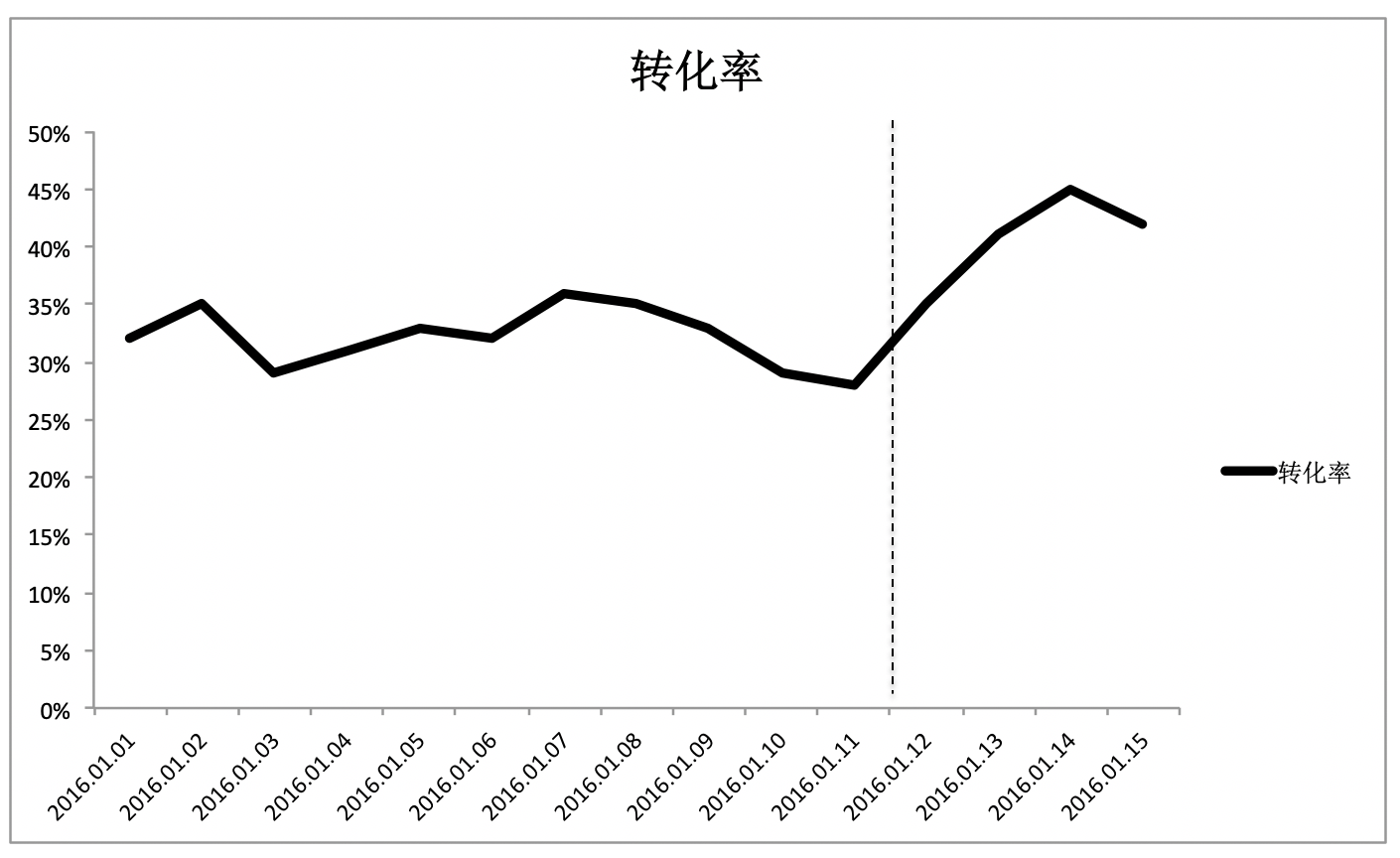
从图中可以看出，自 2016 年 1 月 12 日开始，转化率曲线的趋势发生了明显的变化。假如说这天恰好上线了一个新版的技术方案 A，那么转化率上涨一定是新方案导致的吗？不一定吧？很有可能，1 月 12 日有个大型的促销，使得价格有大幅下降，或者有个和大型企业的合作引入了很多优质顾客等，原因有非常多。如果我们取消 12 日上线的技术方案 A，然后用虚线表示在这种情况下的转化率曲线，这个时候得到了另一张图。
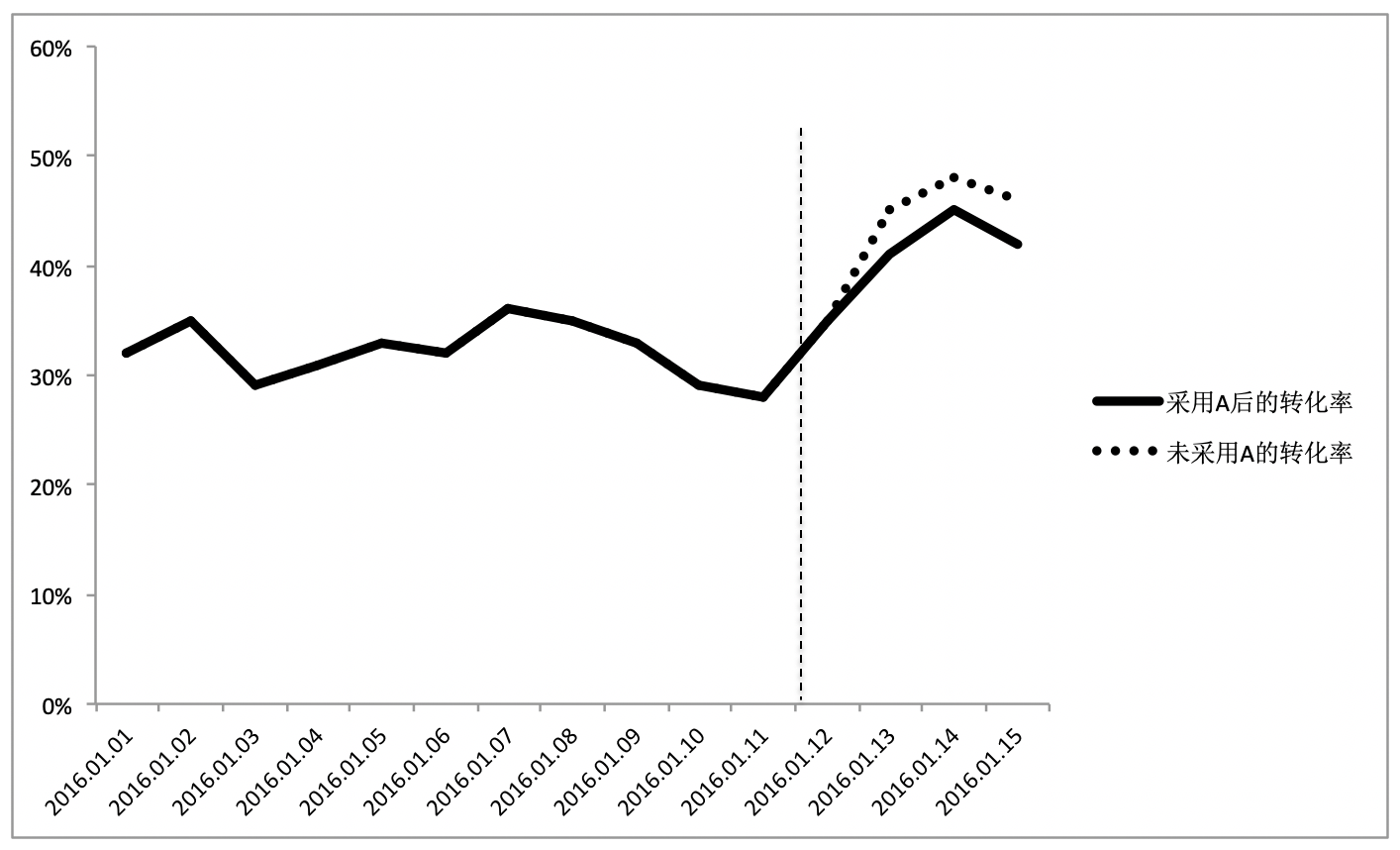
从图中可以发现，不用方案 A，反而获得了更好的转化率表现，所以，简单地使用在线测试的结果往往会导致错误的结论，我们需要一个更健壮的测试方法，A/B 测试。
A/B 测试，简单来说，就是为同一个目标制定两个或多个方案，让一部分用户使用 A 方案，另一部分用户使用 B 方案，记录下每个部分用户的使用情况，看哪个方案产生的结果更好。这也意味着，通过 A/B 测试的方式，我们可以拿到使用多个不同方法之后所产生的多组结果，用于对比。
公开
同步至部落
取消
完成
0/2000
荧光笔
直线
曲线笔记
复制
AI
- 深入了解
- 翻译
- 解释
- 总结
A/B测试是互联网公司常见的实验方法，用于比较不同算法的效果。在A/B测试中，显著性检验是一种重要的统计学方法，用来判断不同方案的效果是否巧合。通过P值的计算，我们可以确定观测值与假设H0的期望值的偏离程度，从而判断是否拒绝原假设。显著性检验和P值的运用可以帮助我们更科学地评估A/B测试结果，避免错误的结论。文章还介绍了显著性差异、统计假设检验和P值的概念，以及它们在实际应用中的重要性。通过形象的比喻和思考题，读者可以更好地理解这些概念。总的来说，本文通过深入浅出的方式，为读者解释了A/B测试中的统计学方法，为他们在实际应用中提供了有益的指导。
仅可试看部分内容，如需阅读全部内容，请付费购买文章所属专栏
《程序员的数学基础课》，新⼈⾸单¥68
《程序员的数学基础课》，新⼈⾸单¥68
立即购买
© 版权归极客邦科技所有，未经许可不得传播售卖。 页面已增加防盗追踪，如有侵权极客邦将依法追究其法律责任。
登录 后留言
全部留言(14)
- 最新
- 精选
yaya我觉得会逐渐变得一致的。样本数量越多，样本均值应该越来越接近于总体均值作者回复: 是的
2019-02-22312- lianlian老师早上好啊！在“总结”的上一段写着“如果P值足够小，我们就可以拒绝原假设，认为多个分组内的数据来自不同的数据分布，它们之间存在显著性的差异。”这里，我的理解是，“存在差异的显著性”。请问我的理解对吗？
作者回复: 是的👌
2019-02-2224 
Ronnyz
样本越大，得到的结果会越趋于平均值，和显著性检验的结论会变得一致。 在假设检验中，当h0成立，而接受h1时，弃真。当h0不成立，而接受h0时，存伪。作者回复: 很好的总结，弃真和存伪就是我们常说的type1 error和type2 error
2019-10-1523- Paul Shan思考题 样本数量增加，如果是正态分布，均值测量会越来越可靠，其差异也会越来越精确，但是仅仅靠均值无法完整描述分布，还要考虑方差。如果不是正态分布，情况就会更为复杂。
作者回复: 是的👍
2019-09-163 - Paul Shan显著性差异 差异具有显著性表示差异的原因是分布差异 具有显著性差异表示差异的绝对值比较大 统计假设检验，先假设，然后看有没有反面证据（在假设条件下的小概率事件），如果有就拒绝原假设，接受对立假设。如果没有就接受原假设。这里拒绝原假设的论证手法和反证法类似。 P值就是在给定假设，观察值发生的概率。这个条件概率越大，假设越可靠。
作者回复: 确切的说，P值是指在空假设（原假设）成立的情况下，给定值发生的概率，如果越小，证明发生的概率越小，越具有偶然性，所以可以更有信心的拒绝空假设。
2019-09-163 - 201201904前面的概念有点抽象，如果先讲儿子考试的例子会更容易理解一些，这就是观测到的不一定准确，还需要一个指标来衡量观测值的可相信程度。
作者回复: 感谢建议，我们后面看下如何调整一下内容
2021-07-1322 
罗耀龙@坐忘
茶艺师学编程 思考题：在对比两组数据的差异时，如果不断增加采样次数，也就是样本的数量，使用平均值和使用显著性检验这两者的结论，会不会逐渐变得一致？ 增加采集次数（样本数量）所得出的平均值，是能趋近整体的平均值……问题是在于平均值能描述出数据本身是如何分布吗？ 因此我觉得在均值层面，增加采集次数的平均值和使用显著性检验得出的结论趋近相同，在整体来看前者只是后者结论的一部分。作者回复: 如果两者都是正态分布，可以这么认为
2020-04-222- Geek_36d3e5文中讲到采样导致的错误，那怎样的样本数量就不会导致了呢？一般线上ab桶各5%流量，总样本量已经很大了，看人均ctr，人均消费时长这种数据数据时，仍会存在这种采样的错误吗？主要是因为每个人每天消费pv或点击的样本数少于30？
作者回复: 很好的问题，统计学里有定义统计意义，也就是说在是否具有统计意义。
2023-02-18归属地：北京1 - 013923学完了，谢谢老师！
作者回复: 很高兴对你有所帮助
2022-09-05归属地：美国1 
建强我的理解是分为两种情况： 第一种，如果两组数据来自同一分布，那么随着样本数的增加，两组数的均值分逐渐靠近，使用显著性检验的P值也会一致，则两者得到的结论是一致的； 第二种，如果两组数据来自不同的分布，随着样本数的增加，可能两组数的均值也会逐渐靠近，但两组数据使用显著性检验的P值肯定会明显不一致，因此不同分布的情况下，两者的结论可能是不一致的。作者回复: 第一种，P值会增大，表示两者不同更有可能是采样的偶然性产生。 第二种，P值会减少，表示两者的不同由偶然性产生的可能性很小，两者应该是来自不同的数据分布
2020-07-121
收起评论
