10 | 动态规划(下):如何求得状态转移方程并进行编程实现?

该思维导图由 AI 生成,仅供参考
状态转移方程和编程实现
- 深入了解
- 翻译
- 解释
- 总结

动态规划在实际问题中的应用是本文的重点。首先,通过编辑距离和钱币组合问题的案例,生动展示了动态规划的思想和实际编程实现。文章详细介绍了状态转移方程的推导过程,并给出了具体的实现方法,帮助读者理解动态规划的应用。作者还提供了编辑距离的Java编程示例,进一步展示了动态规划在实际编码中的应用。其次,针对钱币组合问题,作者通过分解问题、推导状态转移方程和绘制状态转移表的方式,阐述了动态规划的应用场景。最后,文章总结了动态规划的应用经验,指出了在解决问题时应该考虑使用动态规划的情况,并提出了思考题,引发读者的思考和交流。整体而言,本文通过具体案例和编程实现,生动地展示了动态规划在实际问题中的应用,为读者提供了深入理解和实践的机会。
《程序员的数学基础课》,新⼈⾸单¥68
全部留言(104)
- 最新
- 精选
- cwtxz中国程序员的最大阻碍是语言障碍,英语不好,无法和世界各地的人交流技术,坐井观天的人很多。第二个严重的问题就是学习能力不强而且没有毅力,很容易放弃,不肯花时间深入思考问题和钻研,大多思考如何能少加班,如何能赚更多,如何在工作中偷懒等等。第三个问题就是好高骛远不能脚踏实地,很多人刚毕业就想要很多钱,换一份工作就想涨很多钱,但是能力不够,基础不扎实,有些连在简历中写的技术都说不清楚。曾经我是他们中的一员,但是我想改变去,不想继续平庸下去,所以,我来了,加油,坚持坚持再坚持!!!
作者回复: 我很佩服你有如此的思考,坚信自己选择的方向,从脚下的路开始,你一定会得到属于自己的成功
2019-12-28317  Joe1.C++实现,对总金额100的最小纸币是15. 2.用递归法总金额为30就要算很久。 3.另外的数学办法可以用总金额依次对最大金额纸币求余数,直到为0.商相加为答案。如:若 {1, 2, 3, 7}为纸币金额,对于100,所需最小纸币数:100/7=14余2; 2/2 = 1余0;则纸币数为14+1=15. // 动态规划问题 #include <iostream> #include <string> #include <vector> using namespace std; class DynamicProgramming { private: vector<int> money = {1, 2, 3, 7}; // 纸币种类 public: /** * Description: 对于金额固定,找出最少钱币数及方式。 * prams: amountMoney- 输入总金额 * return: 所需最小纸币数 */ int findFewerstMethod(int amountMoney) { int c[amountMoney]; c[0] = 0; int temp; for (unsigned int i = 1; i < amountMoney; i++) { // 用最大值初始化 int tempMin = amountMoney; for (unsigned int j = 0; j < money.size(); j++) { int diff = i - money[j]; if (0 <= diff) { temp = c[diff] + 1; } else { // 此情况表示该纸币无效,选择最大值。 temp = amountMoney; } // 求出最小值 if (temp < tempMin) { tempMin = temp; } } c[i] = tempMin; } return c[amountMoney - 1]; } }; // test int main(void) { DynamicProgramming test; int res = test.findFewerstMethod(100); cout << res << endl; return 0; }
Joe1.C++实现,对总金额100的最小纸币是15. 2.用递归法总金额为30就要算很久。 3.另外的数学办法可以用总金额依次对最大金额纸币求余数,直到为0.商相加为答案。如:若 {1, 2, 3, 7}为纸币金额,对于100,所需最小纸币数:100/7=14余2; 2/2 = 1余0;则纸币数为14+1=15. // 动态规划问题 #include <iostream> #include <string> #include <vector> using namespace std; class DynamicProgramming { private: vector<int> money = {1, 2, 3, 7}; // 纸币种类 public: /** * Description: 对于金额固定,找出最少钱币数及方式。 * prams: amountMoney- 输入总金额 * return: 所需最小纸币数 */ int findFewerstMethod(int amountMoney) { int c[amountMoney]; c[0] = 0; int temp; for (unsigned int i = 1; i < amountMoney; i++) { // 用最大值初始化 int tempMin = amountMoney; for (unsigned int j = 0; j < money.size(); j++) { int diff = i - money[j]; if (0 <= diff) { temp = c[diff] + 1; } else { // 此情况表示该纸币无效,选择最大值。 temp = amountMoney; } // 求出最小值 if (temp < tempMin) { tempMin = temp; } } c[i] = tempMin; } return c[amountMoney - 1]; } }; // test int main(void) { DynamicProgramming test; int res = test.findFewerstMethod(100); cout << res << endl; return 0; }作者回复: 答案正确 👍
2019-01-14414- 云开还是弄不明白编辑距离 为什么插入时是从空串开始 替换确并不计算从空串到有字符的过程
作者回复: 你可以参考那张状态转移表,看看是从哪一格到哪一格,字符串是如何变换的,相邻格子的变换就三种方式,插入、删除和替换。替换可以将字符串中的某个字符替换成另一个字符
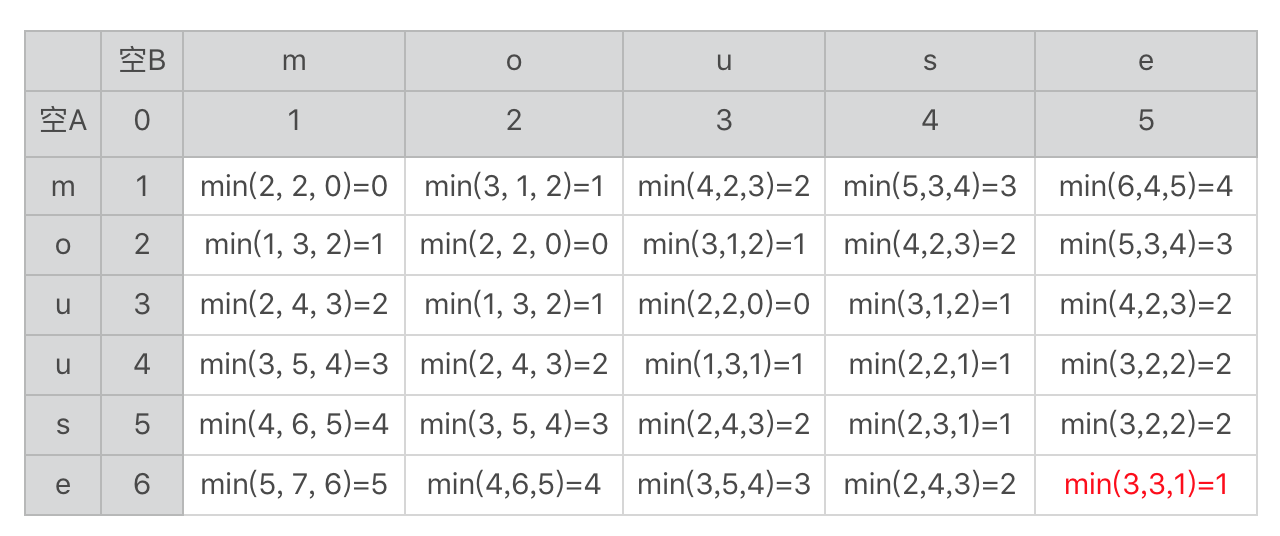
2019-01-3113  冰木老大,我可能没有得到要领,可以推到下,表格中,第一行,第二列吗?
冰木老大,我可能没有得到要领,可以推到下,表格中,第一行,第二列吗?作者回复: 是min(3, 1, 2)对吧,这个是mo和m的比较,3表示增加一个m再增加一个o,再删掉一个o,编辑距离是2+1=3。1表示两个字符串都是m,其中一个再增加一个o,编辑距离是1。2表示一个m增加o,一个从空集到m,编辑距离是2。你可以顺着第9讲最后的表格来推导。
2019-01-2639- 梅坊帝卿按照面值排序优先取最大的方法 不一定能取到解 除非有万能的面额1 比如 2 5 7 总数15
作者回复: 是的 可能无解👍
2019-01-046  予悠悠用python交作业 用递归来实现时,运行非常慢。用循环实现时,由于记录了每一步的计算结果,不需要重复计算,速度快很多。 递归: import sys def least_bills_recursion(total): if total == 0: return 0 if total < 0: return sys.maxint min_bills = min(1 + least_bills_recursion(total-2), 1 + least_bills_recursion(total - 3), 1 + least_bills_recursion(total-7)) return min_bills 循环: def least_bills_iteration(total): current = 0 dp = [0] * (total + 1) dp[2] = 1 dp[3] = 1 dp[7] = 1 for i in xrange(3, total+1, 1): if i >= 7: dp[i] = min(dp[i-2], dp[i-3], dp[i-7]) + 1 elif i >= 3 and i < 7: dp[i] = min(dp[i-2], dp[i-3]) + 1 else: dp[i] = dp[i-2] + 1 return dp[total] 当总金额为100时,答案为15.
予悠悠用python交作业 用递归来实现时,运行非常慢。用循环实现时,由于记录了每一步的计算结果,不需要重复计算,速度快很多。 递归: import sys def least_bills_recursion(total): if total == 0: return 0 if total < 0: return sys.maxint min_bills = min(1 + least_bills_recursion(total-2), 1 + least_bills_recursion(total - 3), 1 + least_bills_recursion(total-7)) return min_bills 循环: def least_bills_iteration(total): current = 0 dp = [0] * (total + 1) dp[2] = 1 dp[3] = 1 dp[7] = 1 for i in xrange(3, total+1, 1): if i >= 7: dp[i] = min(dp[i-2], dp[i-3], dp[i-7]) + 1 elif i >= 3 and i < 7: dp[i] = min(dp[i-2], dp[i-3]) + 1 else: dp[i] = dp[i-2] + 1 return dp[total] 当总金额为100时,答案为15.作者回复: 实现了两种方法,并进行了对比,赞👍
2019-01-2225 我心留public class Lesson10_2 { /** * 动态规划求最小钱币数 * @param c 用一维数组记录每一步的总金额 * @param value 用一维数组记录三种面额的纸币 * @return */ public static int getMinMoney(int[] c, int[] value) { int[] t = new int[3]; for (int i = 0; i < c.length; i++) { for (int j = 0; j < value.length; j++) { if (i - value[j] >= 0) { t[j] = c[i - value[j]] + 1; } } int min = Math.min(t[0], t[1]); min = Math.min(min, t[2]); c[i] = min; } return c[c.length - 1]; } public static void main(String[] args) { int[] c = new int[100]; int[] value = new int[] { 2, 3, 7 }; System.out.println(getMinMoney(c, value)+1); } } 老师看一下代码对吗,运行结果是15
我心留public class Lesson10_2 { /** * 动态规划求最小钱币数 * @param c 用一维数组记录每一步的总金额 * @param value 用一维数组记录三种面额的纸币 * @return */ public static int getMinMoney(int[] c, int[] value) { int[] t = new int[3]; for (int i = 0; i < c.length; i++) { for (int j = 0; j < value.length; j++) { if (i - value[j] >= 0) { t[j] = c[i - value[j]] + 1; } } int min = Math.min(t[0], t[1]); min = Math.min(min, t[2]); c[i] = min; } return c[c.length - 1]; } public static void main(String[] args) { int[] c = new int[100]; int[] value = new int[] { 2, 3, 7 }; System.out.println(getMinMoney(c, value)+1); } } 老师看一下代码对吗,运行结果是15作者回复: 代码的逻辑是对的
2019-01-0524- lianlian方法1,动态规划,最快。方法2递归有点慢,方法三递归,超级慢。在aim数值大于30的时候,三种写法,在我电脑速度快慢特别明显。用2元,3元,5元去找开100块,用递归方法,我的电脑要等到地老天荒O(∩_∩)O哈哈~ #include<iostream> #include<vector> using namespace std; int dp_solve(int *a, int n, int aim){ vector<vector<int>> dp(n, vector<int>(aim+1, 0)); for(int j = 1; j <= aim; j++){ dp[0][j] = INT_MAX; if(j >= a[0] && dp[0][j - a[0]] != INT_MAX) dp[0][j] = dp[0][j - a[0]] + 1; } for(int i = 1; i < n; i++){ for(int j = 1; j <= aim; j++) { int tmp = INT_MAX; if(j - a[i] >= 0 && dp[i][j - a[i]] != INT_MAX) tmp = dp[i][j - a[i]] + 1; dp[i][j] = min(dp[i-1][j], tmp); } } return dp[n-1][aim] == INT_MAX ? -1 : dp[n-1][aim]; } int min_res = INT_MAX; void recur_solve(int *a, int n, int aim, int k){ if(aim == 0){ min_res = min(min_res, k); return; } if(aim < 0) return; for(int i = 0; i < n; i++){ aim -= a[i]; k++; recur_solve(a, n, aim, k); aim += a[i]; k--; } } int min_res2 = INT_MAX; void recur_solve2(int *a, int n, int aim, vector<int> res){ if(aim == 0){ int size = res.size(); min_res2 = min(min_res2, size); return; } if(aim < 0) return; for(int i = 0; i < n; i++){ res.push_back(a[i]); recur_solve2(a, n, aim - a[i], res); res.pop_back(); } } int main(){ int a[] = {2,3,7}; int sum = 25; /***dp最快**/ cout << dp_solve(a, 3, sum) << endl; /***这种递归有点久**/ recur_solve(a, 3, sum, 0); cout << min_res << endl; /**这个太久了**/ vector<int> result; recur_solve2(a, 3, sum, result); cout << min_res2 << endl; return 0; }
作者回复: 动手实验,比较不同的实现,👍
2019-01-044 - 木子皿动态规划的这两篇文章看了一个星期,总算是看懂了!
作者回复: 确实不太好理解,不过一旦理解了对解题很有帮助
2019-10-1922  别人家的康少说到动态规划,你说是考虑当前子问题的最优解,我于是想到了贪心算法,请问这两者有什么区别呢
别人家的康少说到动态规划,你说是考虑当前子问题的最优解,我于是想到了贪心算法,请问这两者有什么区别呢作者回复: 动态规划虽然是当前子问题的最优解,不过由于不断的通过子问题递推到整个问题,其实是完成了对所有解的搜索,只是通过状态转移方程,缩减了很多不必要的搜索路径,是可以得到全局最优的。而贪心算法的本质决定了到达一定条件后就停止搜索,而全局最优解可能会存在于未被搜索的空间之中。简单来理解,动态规划确实搜索了所有的可能,只是在一定程度上提升了效率。而贪心可能效率更高,但是遗漏了全局最优。
2020-12-081

