13 | 树的广度优先搜索(上):人际关系的六度理论是真的吗?
黄申

该思维导图由 AI 生成,仅供参考
你好,我是黄申。
上一节,我们探讨了如何在树的结构里进行深度优先搜索。说到这里,有一个问题,不知道你有没有思考过,树既然是两维的,我们为什么一定要朝着纵向去进行深度优先搜索呢?是不是也可以朝着横向来进行搜索呢?今天我们就来看另一种搜索机制,广度优先搜索。
社交网络中的好友问题
LinkedIn、Facebook、微信、QQ 这些社交网络平台都有大量的用户。在这些社交网络中,非常重要的一部分就是人与人之间的“好友”关系。
在数学里,为了表示这种好友关系,我们通常使用图中的结点来表示一个人,而用图中的边来表示人和人之间的相识关系,那么社交网络就可以用图论来表示。而“相识关系”又可以分为单向和双向。
单向表示,两个人 a 和 b,a 认识 b,但是 b 不认识 a。如果是单向关系,我们就需要使用有向边来区分是 a 认识 b,还是 b 认识 a。如果是双向关系,双方相互认识,因此直接用无向边就够了。在今天的内容里,我们假设相识关系都是双向的,所以我们今天讨论的都是无向图。
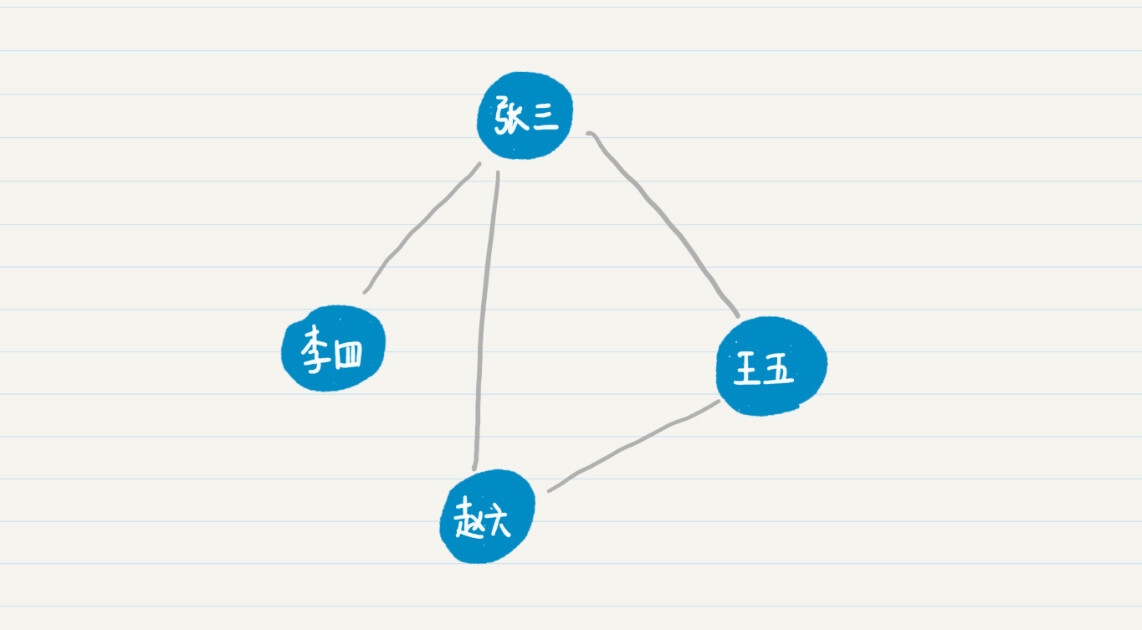
从上面的例图可以看出,人与人之间的相识关系,可以有多条路径。比如,张三可以直接连接赵六,也可以通过王五来连接赵六。比较这两条通路,最短的通路长度是 1,因此张三和赵六是一度好友。也就是说,这里我用两人之间最短通路的长度,来定义他们是几度好友。照此定义,在之前的社交关系示意图中,张三、王五和赵六互为一度好友,而李四和赵六、王五为二度好友。
公开
同步至部落
取消
完成
0/2000
笔记
复制
AI
- 深入了解
- 翻译
- 解释
- 总结

本文介绍了社交网络中的好友关系表示方法以及如何使用广度优先搜索来寻找好友关系。文章首先讨论了深度优先搜索在寻找好友关系中可能遇到的问题,以及为什么广度优先搜索是更高效的方法。接着详细介绍了广度优先搜索的原理和特点,并通过图示和比较展示了广度优先搜索和深度优先搜索的不同之处。最后,强调了广度优先搜索的优势,特别是在涉及多个连通子图的情况下。文章还提供了代码示例,演示了如何使用队列来实现广度优先搜索。总的来说,本文通过介绍人际关系的六度理论和广度优先搜索在社交网络中的应用,为读者提供了基础理论和实际操作的结合,帮助读者快速了解并应用这一技术。
仅可试看部分内容,如需阅读全部内容,请付费购买文章所属专栏
《程序员的数学基础课》,新⼈⾸单¥68
《程序员的数学基础课》,新⼈⾸单¥68
立即购买
© 版权归极客邦科技所有,未经许可不得传播售卖。 页面已增加防盗追踪,如有侵权极客邦将依法追究其法律责任。
登录 后留言
全部留言(17)
- 最新
- 精选

 罗耀龙@坐忘
罗耀龙@坐忘 茶艺师学编程 一张由节点和边构成的图如何遍历? 在学完“一条路走到黑”的深度优先搜索(DFS)后,今天我们迎来另一种遍历算法:广度优先搜索(BFS)。 我把她理解为:谁和我最亲近? 其实,广度优先搜索这思想早已是我们生活的一部分。 费孝通先生用“差序格局”来形容我们中国的古代社会,其中作为主骨的儒家思想,其“创始人”孔子教导道:修身齐家治国平天下(先把自己管好,再把自己家事处理好,然后才是国家、天下)。 在西方,(神话)经济学之父亚当斯密也有类似的洞见,他说 “正因为人的同情心就那么一点点,他肯定会优先自己,然后是家人、朋友,再然后才是同一条街的领居……也正因为这样,当要与更远的陌生人发生协作时,这时候就需要市场来协调……” 这些,其底层的数学原理,正是今天所讲的广度优先搜索。 而各位程序员大神把这*教*给了计算机,让它反过来帮助人类处理更加复杂的问题。
茶艺师学编程 一张由节点和边构成的图如何遍历? 在学完“一条路走到黑”的深度优先搜索(DFS)后,今天我们迎来另一种遍历算法:广度优先搜索(BFS)。 我把她理解为:谁和我最亲近? 其实,广度优先搜索这思想早已是我们生活的一部分。 费孝通先生用“差序格局”来形容我们中国的古代社会,其中作为主骨的儒家思想,其“创始人”孔子教导道:修身齐家治国平天下(先把自己管好,再把自己家事处理好,然后才是国家、天下)。 在西方,(神话)经济学之父亚当斯密也有类似的洞见,他说 “正因为人的同情心就那么一点点,他肯定会优先自己,然后是家人、朋友,再然后才是同一条街的领居……也正因为这样,当要与更远的陌生人发生协作时,这时候就需要市场来协调……” 这些,其底层的数学原理,正是今天所讲的广度优先搜索。 而各位程序员大神把这*教*给了计算机,让它反过来帮助人类处理更加复杂的问题。作者回复: 你的比方都很形象👍
2020-04-05211- cwtxz编程这么些年,就从来没有把递归相关的编程问题克服过。虽然天天加班,但是一直都在做一些重复的业务,遇到一些稍微麻烦的问题,下意识的就会去网上搜索现成的解决方案,久而久之,自己独立分析思考问题的能力变得羸弱不堪。一旦遇到一些稍微抽象一点、分析步骤稍微繁琐的问题,往往找不到破解问题的方向,坚持不了多久就容易心浮气躁,心生放弃。所以,类似递归这类抽象度高又复杂的算法,本能地会畏惧,敬而远之。但是,男人不能怂,这次我不能避而不战了,我一定要克服递归,无论多难,我都不想放弃!!!加油!!!
作者回复: 相信你可以做到的,新年新气象👍
2019-12-3137  strentchRise自己代码功力不行,尽力写一个python版本的 class Node: def __init__(self, number): self.num = number self.nodes = [] def setNode(self, num): if(self.nodes.__contains__(num) == False): node = Node(num) self.nodes.append(node) return node else: return None def setNodeUnder(self, num, base): if (self.num == num): return self.setNode(num) baseNode = self.get(base, self.nodes) if baseNode == None: return None else: return baseNode.setNode(num) def get(self, num, nodes=None): if(self.nodes == None or len(nodes) == 0): return None else: someNodes = [] for node in nodes: if node.num == num: return node for n in node.nodes: someNodes.append(n) return self.get(num, someNodes) def search(self): print(self.num) self.printNodes(self.nodes) def printNodes(self, nodes=None): if nodes == None or len(nodes) == 0: return else: someNodes = [] for node in nodes: print(node.num) for n in node.nodes: someNodes.append(n) return self.printNodes(someNodes) root = Node(110) root.setNode(123) root.setNode(879) root.setNode(945) root.setNode(131) root.setNodeUnder(162, 123) root.setNodeUnder(587, 123) root.setNodeUnder(580, 945) root.setNodeUnder(762, 945) root.setNodeUnder(906, 131) root.setNodeUnder(681, 587) root.search() output: 110 123 879 945 131 162 587 580 762 906 681 finish...
strentchRise自己代码功力不行,尽力写一个python版本的 class Node: def __init__(self, number): self.num = number self.nodes = [] def setNode(self, num): if(self.nodes.__contains__(num) == False): node = Node(num) self.nodes.append(node) return node else: return None def setNodeUnder(self, num, base): if (self.num == num): return self.setNode(num) baseNode = self.get(base, self.nodes) if baseNode == None: return None else: return baseNode.setNode(num) def get(self, num, nodes=None): if(self.nodes == None or len(nodes) == 0): return None else: someNodes = [] for node in nodes: if node.num == num: return node for n in node.nodes: someNodes.append(n) return self.get(num, someNodes) def search(self): print(self.num) self.printNodes(self.nodes) def printNodes(self, nodes=None): if nodes == None or len(nodes) == 0: return else: someNodes = [] for node in nodes: print(node.num) for n in node.nodes: someNodes.append(n) return self.printNodes(someNodes) root = Node(110) root.setNode(123) root.setNode(879) root.setNode(945) root.setNode(131) root.setNodeUnder(162, 123) root.setNodeUnder(587, 123) root.setNodeUnder(580, 945) root.setNodeUnder(762, 945) root.setNodeUnder(906, 131) root.setNodeUnder(681, 587) root.search() output: 110 123 879 945 131 162 587 580 762 906 681 finish...作者回复: 很好的还原了原文的示例👍
2019-01-116
 escray
escray 回过头来重看了一遍,对于树的广度优先搜索,从概念上理解了,但是实际动手写一段 Java 或者是 Python 的代码,还是没有信心。 学习了 @qinggeouye 的 Python 代码 和 @恬毅 的 Java 代码。希望以后自己也能提交一些代码。
回过头来重看了一遍,对于树的广度优先搜索,从概念上理解了,但是实际动手写一段 Java 或者是 Python 的代码,还是没有信心。 学习了 @qinggeouye 的 Python 代码 和 @恬毅 的 Java 代码。希望以后自己也能提交一些代码。作者回复: 反复学习,坚持就可以
2020-02-033 JoeC++实现DFS显示ubuntu指定目录下所有的文件,请老师指点。 #include <dirent.h> #include <stdlib.h> #include <string.h> #include <unistd.h> #include <iostream> #include <regex> #include <stack> using namespace std; class FileSearch { private: stack<string> path; // 路径栈 public: /** * Detail: DFS显示ubuntu指定目录下文件 * basePath- 文件路径 * return: null */ void DfsFile(char *basePath) { DIR *dir; struct dirent *ptr; char base[1000]; char temp[1000]; // 路径入栈 path.push(basePath); // 遍历开始 while (!path.empty()) { // 打开当前目录 strcpy(temp, path.top().c_str()); path.pop(); cout << "Current path: " << temp << endl; if ((dir = opendir(temp)) == NULL) { perror("Open dir error, please input the right path"); exit(1); } // 显示当前路径下的文件 while ((ptr = readdir(dir)) != NULL) { // 忽略隐藏文件和路径: .and.. if (regex_match(ptr->d_name, regex("\\.(.*)"))) { continue; } if (ptr->d_type == 8) { // A regular file //cout << "file: " << basePath << "/" << ptr->d_name << endl; cout << ptr->d_name << endl; } else if (ptr->d_type == 4) { // 检测为文件夹 memset(base, '\0', sizeof(base)); strcpy(base, temp); strcat(base, "/"); strcat(base, ptr->d_name); path.push(base); continue; } } } // 关闭文件 closedir(dir); } }; int main(void) { FileSearch test; // 需要遍历的文件夹目录 char basePath[] = {"/home/joe/Desktop/leetcode"}; test.DfsFile(basePath); return 0; } // 大致输出结果为: Current path: /home/joe/Desktop/leetcode leetcodePractice.cpp a.out README.md Current path: /home/joe/Desktop/leetcode/math_fundamental_algorithms recursion.cpp tree_depth_first_search.cpp recursion_integer.cpp permutation.cpp dynamic_programming.md iteration_way.cpp tree_breadth_first_search.md a.out tree_breadth_first_search.cpp math_induction.cpp byte_operation.cpp ......
JoeC++实现DFS显示ubuntu指定目录下所有的文件,请老师指点。 #include <dirent.h> #include <stdlib.h> #include <string.h> #include <unistd.h> #include <iostream> #include <regex> #include <stack> using namespace std; class FileSearch { private: stack<string> path; // 路径栈 public: /** * Detail: DFS显示ubuntu指定目录下文件 * basePath- 文件路径 * return: null */ void DfsFile(char *basePath) { DIR *dir; struct dirent *ptr; char base[1000]; char temp[1000]; // 路径入栈 path.push(basePath); // 遍历开始 while (!path.empty()) { // 打开当前目录 strcpy(temp, path.top().c_str()); path.pop(); cout << "Current path: " << temp << endl; if ((dir = opendir(temp)) == NULL) { perror("Open dir error, please input the right path"); exit(1); } // 显示当前路径下的文件 while ((ptr = readdir(dir)) != NULL) { // 忽略隐藏文件和路径: .and.. if (regex_match(ptr->d_name, regex("\\.(.*)"))) { continue; } if (ptr->d_type == 8) { // A regular file //cout << "file: " << basePath << "/" << ptr->d_name << endl; cout << ptr->d_name << endl; } else if (ptr->d_type == 4) { // 检测为文件夹 memset(base, '\0', sizeof(base)); strcpy(base, temp); strcat(base, "/"); strcat(base, ptr->d_name); path.push(base); continue; } } } // 关闭文件 closedir(dir); } }; int main(void) { FileSearch test; // 需要遍历的文件夹目录 char basePath[] = {"/home/joe/Desktop/leetcode"}; test.DfsFile(basePath); return 0; } // 大致输出结果为: Current path: /home/joe/Desktop/leetcode leetcodePractice.cpp a.out README.md Current path: /home/joe/Desktop/leetcode/math_fundamental_algorithms recursion.cpp tree_depth_first_search.cpp recursion_integer.cpp permutation.cpp dynamic_programming.md iteration_way.cpp tree_breadth_first_search.md a.out tree_breadth_first_search.cpp math_induction.cpp byte_operation.cpp ......作者回复: 注意到了隐藏路径和文件的处理,很棒
2019-01-203- 杨芸芸1、采用广度优先搜索BFS算法,像剥洋葱一样一层层搜索每一层路径下的文件和目录。使用两个队列,一个队列存储待继续搜索的目录和文件,一个队列存储搜索到的结果文件和目录,知道第一个队列为空则搜索结束。 2、也可以使用深度优先搜索算法DFS,使用栈存储待搜索的目录或文件,采用迭代的方式:把某一个路径搜索到底然后返回父目录,继续搜索父目录的其他子目录或文件,不断重复这个过程直到栈为空
作者回复: 是的,不过要看具体需求和应用场景。
2023-01-02归属地:湖北1  抱紧我的小鲤鱼曾经面试遇到过这个问题,现在豁然开朗
抱紧我的小鲤鱼曾经面试遇到过这个问题,现在豁然开朗作者回复: 很高兴对你有帮助!
2022-06-22- 菩提我好好检查了一下我的代码逻辑,您的逻辑是正确的。 我这边visited集合没有把user_id加入,导致的问题。 控制台的输出日志。我查询的是user_id是 0, 而控制台打印了一行记录是 2度好友:0 。 出现这个打印的原因是遍历0的好友。该好友的friends包含了0,在for循环中算了user_id=0的情况。 谢谢老师指正!
作者回复: 找到问题就好👍
2019-01-16 - 菩提广度优先搜索那块有2个小瑕疵,您看一下。 1. 防止数组越界的异常,user_id 等于数组长度也会越界。 2.遍历子节点的时候,如果子节点friends中存在需要查询的user_id,则出现错误的打印输出。如果是查询的user_id应该continue。 控制台打印 0:[3]:0 1:[3]:0 2:[3]:0 3:[0, 1, 2, 4]:0 4:[3]:0 1 度好友:3 2 度好友:0 2 度好友:1 2 度好友:2 2 度好友:4 代码如下, public static Node[] init(int user_num, int relation_num) { Random rand = new Random(); Node[] user_nodes = new Node[user_num]; // 生成所有表示用户的节点 for (int i = 0; i < user_num; i++) { user_nodes[i] = new Node(i); } // 生成所有表示好友关系的边 for (int i = 0; i < relation_num; i++) { int friend_a_id = rand.nextInt(user_num); int friend_b_id = rand.nextInt(user_num); if (friend_a_id == friend_b_id) continue; Node friend_a = user_nodes[friend_a_id]; Node friend_b = user_nodes[friend_b_id]; friend_a.friends.add(friend_b_id); friend_b.friends.add(friend_a_id); } return user_nodes; } public static void bfs(Node[] user_nodes, int user_id) { // 防止数组越界异常 if (user_id >= user_nodes.length) return; // 用于广度优先搜索的队列 Queue<Integer> queue = new LinkedList<>(); // 放入初始节点 queue.offer(user_id); // 存放已经被访问过的节点,防止回路 HashSet<Integer> visited = new HashSet<>(); while (!queue.isEmpty()) { // 取出队列头部的第一个节点 int current_user_id = queue.poll(); if (user_nodes[current_user_id] == null) continue; // 遍历刚刚拿到的这个节点的所有直接连接节点,并加入队列尾部 for (int friend_id : user_nodes[current_user_id].friends) { if (user_nodes[current_user_id] == null) continue; if (visited.contains(friend_id)) continue; queue.offer(friend_id); // 记录已经访问过的节点 visited.add(friend_id); // 好友度数是当前节点的好友度数再加1 user_nodes[friend_id].degree = user_nodes[current_user_id].degree + 1; System.out.println(String.format("\t%d 度好友:%d", user_nodes[friend_id].degree, friend_id)); } } } public static void main(String[] args) { Node[] user_nodes = init(5, 8); for (Node d : user_nodes) { System.out.println(d.user_id + ":" + d.friends + ":" + d.degree); } bfs(user_nodes, 0); }
作者回复: 第一点是很好的发现,我稍后加一下。 第二点没有看太明白,能否补充说明一下?
2019-01-15  Being使用C++的双端队列deque实现的BFS和DFS namespace FilePathOperator { struct St_FilePathNode; typedef std::set<St_FilePathNode*> SetterFilePathNode; typedef void(*FilPathOperator)(const St_FilePathNode& rStFilePathNode); typedef struct St_FilePathNode { int m_nLevel; std::string m_strFilePath; SetterFilePathNode m_setChildernPathNodes; }StFilePathNode; }; void FilePathOperator::BFSFilePathNodes(StFilePathNode * pRoot, FilPathOperator nodeOperator, int nMaxLevel) { if (NULL == pRoot) return; std::deque<StFilePathNode*> queNode; queNode.push_front(pRoot); pRoot->m_nLevel = 0; // Root Level is first one while (!queNode.empty()) { StFilePathNode* pNode = queNode.back(); queNode.pop_back(); if (NULL == pNode) continue; int nNodeLevel = pNode->m_nLevel; nodeOperator(*pNode); if (nNodeLevel + 1 > nMaxLevel) continue; // childern beyond MaxLevel SetterFilePathNode::iterator ChildItr = pNode->m_setChildernPathNodes.begin(); for (; ChildItr != pNode->m_setChildernPathNodes.end(); ChildItr++) { if (NULL == *ChildItr) continue; (*ChildItr)->m_nLevel = nNodeLevel + 1; queNode.push_front(*ChildItr); } } } void FilePathOperator::DFSFilePathNodes(StFilePathNode * pRoot, FilPathOperator nodeOperator, int nMaxLevel) { if (NULL == pRoot) return; std::deque<StFilePathNode*> deqNode; deqNode.push_front(pRoot); pRoot->m_nLevel = 0; // Root Level is first one while (!deqNode.empty()) { StFilePathNode* pNode = deqNode.front(); deqNode.pop_front(); if (NULL == pNode) continue; int nNodeLevel = pNode->m_nLevel; nodeOperator(*pNode); if (nNodeLevel + 1 > nMaxLevel) continue; // childern beyond MaxLevel SetterFilePathNode::iterator ChildItr = pNode->m_setChildernPathNodes.cbegin(); for (; ChildItr != pNode->m_setChildernPathNodes.cend(); ChildItr++) { if (NULL == *ChildItr) continue; (*ChildItr)->m_nLevel = nNodeLevel + 1; deqNode.push_front(*ChildItr); } } } (其他的Create、Destroy、Print就暂时不贴出来了)
Being使用C++的双端队列deque实现的BFS和DFS namespace FilePathOperator { struct St_FilePathNode; typedef std::set<St_FilePathNode*> SetterFilePathNode; typedef void(*FilPathOperator)(const St_FilePathNode& rStFilePathNode); typedef struct St_FilePathNode { int m_nLevel; std::string m_strFilePath; SetterFilePathNode m_setChildernPathNodes; }StFilePathNode; }; void FilePathOperator::BFSFilePathNodes(StFilePathNode * pRoot, FilPathOperator nodeOperator, int nMaxLevel) { if (NULL == pRoot) return; std::deque<StFilePathNode*> queNode; queNode.push_front(pRoot); pRoot->m_nLevel = 0; // Root Level is first one while (!queNode.empty()) { StFilePathNode* pNode = queNode.back(); queNode.pop_back(); if (NULL == pNode) continue; int nNodeLevel = pNode->m_nLevel; nodeOperator(*pNode); if (nNodeLevel + 1 > nMaxLevel) continue; // childern beyond MaxLevel SetterFilePathNode::iterator ChildItr = pNode->m_setChildernPathNodes.begin(); for (; ChildItr != pNode->m_setChildernPathNodes.end(); ChildItr++) { if (NULL == *ChildItr) continue; (*ChildItr)->m_nLevel = nNodeLevel + 1; queNode.push_front(*ChildItr); } } } void FilePathOperator::DFSFilePathNodes(StFilePathNode * pRoot, FilPathOperator nodeOperator, int nMaxLevel) { if (NULL == pRoot) return; std::deque<StFilePathNode*> deqNode; deqNode.push_front(pRoot); pRoot->m_nLevel = 0; // Root Level is first one while (!deqNode.empty()) { StFilePathNode* pNode = deqNode.front(); deqNode.pop_front(); if (NULL == pNode) continue; int nNodeLevel = pNode->m_nLevel; nodeOperator(*pNode); if (nNodeLevel + 1 > nMaxLevel) continue; // childern beyond MaxLevel SetterFilePathNode::iterator ChildItr = pNode->m_setChildernPathNodes.cbegin(); for (; ChildItr != pNode->m_setChildernPathNodes.cend(); ChildItr++) { if (NULL == *ChildItr) continue; (*ChildItr)->m_nLevel = nNodeLevel + 1; deqNode.push_front(*ChildItr); } } } (其他的Create、Destroy、Print就暂时不贴出来了)作者回复: Deque确实是个好东西,只是名字有时让人联想不到stack :)
2019-01-11
收起评论

