37 | 矩阵(上):如何使用矩阵操作进行PageRank计算?
黄申

该思维导图由 AI 生成,仅供参考
你好,我是黄申。今天我来说说矩阵。
前面我说过,矩阵由多个长度相等的向量组成,其中的每列或者每行就是一个向量。从数据结构的角度来看,我们可以把向量看作一维数组,把矩阵看作二维数组。
具有了二维数组的特性,矩阵就可以表达二元关系了,例如图中结点的邻接关系,或者是用户对物品的评分关系。而通过矩阵上的各种运算操作,我们就可以挖掘这些二元关系,在不同的应用场景下达到不同的目的。今天我就从图的邻接矩阵出发,展示如何使用矩阵计算来实现 PageRank 算法。
回顾 PageRank 链接分析算法
在讲马尔科夫模型的时候,我已经介绍了 PageRank 链接分析算法。所以,在展示这个算法和矩阵操作的关系之前,我们快速回顾一下它的核心思想。
PageRank 是基于马尔科夫链的。它假设了一个“随机冲浪者”模型,冲浪者从某张网页出发,根据 Web 图中的链接关系随机访问。在每个步骤中,冲浪者都会从当前网页的链出网页中,随机选取一张作为下一步访问的目标。此外,PageRank 还引入了随机的跳转操作,这意味着冲浪者不是按 Web 图的拓扑结构走下去,只是随机挑选了一张网页进行跳转。
基于之前的假设,PageRank 的公式定义如下:
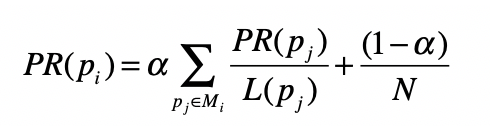
其中, 表示第 张网页, 是 的入链接集合, 是 集合中的第 张网页。 表示网页 的 PageRank 得分, 表示网页 的出链接数量, 就表示从网页 跳转到 的概率。 是用户不进行随机跳转的概率, 表示所有网页的数量。
公开
同步至部落
取消
完成
0/2000
笔记
复制
AI
- 深入了解
- 翻译
- 解释
- 总结

本文深入介绍了如何使用矩阵操作进行PageRank计算,通过简洁清晰的语言和具体的示例,帮助读者快速了解了PageRank算法与矩阵操作的关系,以及如何使用Python实现PageRank计算。文章首先回顾了PageRank链接分析算法的核心思想,即基于马尔科夫链的随机冲浪者模型。随后,通过简化PageRank公式并与矩阵点乘的计算公式进行对比,展示了如何将PageRank计算转化为矩阵操作。文章还讨论了考虑随机跳转的情况,并通过矩阵的点乘来实现完整的PageRank公式。最后,以Python代码的形式展示了如何利用科学计算语言提供的库来完成基于PageRank的链接分析。此外,文章还提到了矩阵点乘在其他领域的应用,如K均值聚类算法和协同过滤的推荐。整体而言,本文为读者提供了深入的技术细节和实际操作示例,使其能够全面了解PageRank算法与矩阵操作的关系,以及如何应用于实际计算中。
仅可试看部分内容,如需阅读全部内容,请付费购买文章所属专栏
《程序员的数学基础课》,新⼈⾸单¥68
《程序员的数学基础课》,新⼈⾸单¥68
立即购买
© 版权归极客邦科技所有,未经许可不得传播售卖。 页面已增加防盗追踪,如有侵权极客邦将依法追究其法律责任。
登录 后留言
全部留言(10)
- 最新
- 精选
 晨曦后浪使用networkx中的pagerank函数,计算出来的数值和直接基于矩阵计算出来的数值有一点点差别,但相对大小还是一样的 import networkx as nx import matplotlib.pyplot as plt # 创建有向图 G = nx.DiGraph() # 添加带权重有向边 G.add_weighted_edges_from([(1, 3, 1), (2, 1, 1), (2, 3, 1), (3, 1, 1), (5, 2, 1)]) # 添加孤立节点 G.add_node(4) # 计算pagerank值 pagerank_list = nx.pagerank(G, alpha=0.85) print("pagerank 值是:", pagerank_list) nx.draw(G, with_labels=True, font_weight='bold') plt.show() pagerank 值是: {1: 0.43042160902192195, 3: 0.43042160902192195, 2: 0.06686758646711714, 5: 0.03614459774451953, 4: 0.03614459774451953}
晨曦后浪使用networkx中的pagerank函数,计算出来的数值和直接基于矩阵计算出来的数值有一点点差别,但相对大小还是一样的 import networkx as nx import matplotlib.pyplot as plt # 创建有向图 G = nx.DiGraph() # 添加带权重有向边 G.add_weighted_edges_from([(1, 3, 1), (2, 1, 1), (2, 3, 1), (3, 1, 1), (5, 2, 1)]) # 添加孤立节点 G.add_node(4) # 计算pagerank值 pagerank_list = nx.pagerank(G, alpha=0.85) print("pagerank 值是:", pagerank_list) nx.draw(G, with_labels=True, font_weight='bold') plt.show() pagerank 值是: {1: 0.43042160902192195, 3: 0.43042160902192195, 2: 0.06686758646711714, 5: 0.03614459774451953, 4: 0.03614459774451953}作者回复: 赞一下实践精神,确实我也发现了这点,估计是具体实现上有所区别。
2019-03-118 qinggeouye思考题 https://github.com/qinggeouye/GeekTime/blob/master/MathematicProgrammer/37_Matrix2PageRank/lesson37_1.py # 计算前后两次的 PageRank 数值的误差,判断是否需要结束迭代 delta = list(map(abs, (pr/pr_tmp))) # pr_tmp 是前一次的值 delta = abs(np.max(delta) - 1) # 最大误差的百分比 if delta <= delta_threshold: return pr else: continue 经计算,示例最大循环 6 次,迭代结束。 round 6 [[0.46010028 0.03905229 0.46010028 0.02037357 0.02037357]]
qinggeouye思考题 https://github.com/qinggeouye/GeekTime/blob/master/MathematicProgrammer/37_Matrix2PageRank/lesson37_1.py # 计算前后两次的 PageRank 数值的误差,判断是否需要结束迭代 delta = list(map(abs, (pr/pr_tmp))) # pr_tmp 是前一次的值 delta = abs(np.max(delta) - 1) # 最大误差的百分比 if delta <= delta_threshold: return pr else: continue 经计算,示例最大循环 6 次,迭代结束。 round 6 [[0.46010028 0.03905229 0.46010028 0.02037357 0.02037357]]作者回复: 代码实现的很简洁,赞一个
2019-03-235
 罗耀龙@坐忘
罗耀龙@坐忘 茶艺师学编程 可惜我目前还没有能力去跑代码。 但整篇课文消化下来,pagerank这么复杂的函数,用矩阵“嵌套”两层就搞定了……体会到矩阵工具的强大。
茶艺师学编程 可惜我目前还没有能力去跑代码。 但整篇课文消化下来,pagerank这么复杂的函数,用矩阵“嵌套”两层就搞定了……体会到矩阵工具的强大。作者回复: 是的没错
2020-04-304 !null以上两个公式在形式上是基本一致的。。。怎么看出是一致的?简化公式和矩阵点乘公式
!null以上两个公式在形式上是基本一致的。。。怎么看出是一致的?简化公式和矩阵点乘公式作者回复: 详细的说,形式都是多个乘积项的加和
2020-09-111 拉欧一直想搞明白pagerank的计算流程,这节课真值2019-03-1110
拉欧一直想搞明白pagerank的计算流程,这节课真值2019-03-1110- Paul Shan邻接矩阵的行表示每个节点出边,列表示每个节点的入边。行做归一化是为了出边平均分配权重,矩阵的乘法恰好按照入边累加pr值。 随机跳转还是线性关系,依然可以用矩阵处理,这里用到矩阵分块思想。2019-09-2713
 等待pagerank的时间复杂度是O( r * n^ 2),其中,r是指迭代次数。 当数据量达到一定的程度的时候,network联图的建立都无法完成的时候,我们应该如何处理呢? 这里的大数据量大概是300万条数据的样子。谢谢2020-04-0112
等待pagerank的时间复杂度是O( r * n^ 2),其中,r是指迭代次数。 当数据量达到一定的程度的时候,network联图的建立都无法完成的时候,我们应该如何处理呢? 这里的大数据量大概是300万条数据的样子。谢谢2020-04-0112- 013923Never too old to learn!2022-09-14归属地:上海
 建强思考题: 我尝试改了一下老师的代码,把迭代结束条件改为计算前后两次PageRank向量的差的平均值是否小于指定精度,发现这个迭代过程收敛很快,只用了7轮循环就结束了,程序部分代码如下,不当之处请老师指正: # 采样迭代方式,判断前后两次PageRank向量的差的平均值是否小于指定精度。 pricision = 1e-9 # 设置计算精度 last_pr = None i = 0 while True: # 进行点乘,计算Σ(PR(pj)/L(pj)) pr = np.dot(pr, adj) # 转置保存Σ(PR(pj)/L(pj))结果的矩阵,并增加长度为N的列向量,其中每个元素的值为1/N,便于下一步的点乘。 pr_jump = np.full([N, 2], [[0, 1/N]]) pr_jump[:,:-1] = pr.transpose() # 进行点乘,计算α(Σ(PR(pj)/L(pj))) + (1-α)/N) pr = np.dot(pr_jump, jump) # 归一化PageRank得分,由于计算后pr是列向量,因此需要做转置 pr = pr.transpose() pr = pr / pr.sum() print("round", i + 1, pr) if last_pr is not None: diff = np.average(np.absolute(pr - last_pr)) if diff <= pricision: break last_pr = pr.copy() i += 1 ############程序输出############# round 1 [[0.37027027 0.24864865 0.37027027 0.00540541 0.00540541]] round 2 [[0.46740902 0.02498642 0.46740902 0.02009777 0.02009777]] round 3 [[0.46023676 0.03878962 0.46023676 0.02036842 0.02036842]] round 4 [[0.46010283 0.03904738 0.46010283 0.02037348 0.02037348]] round 5 [[0.46010033 0.0390522 0.46010033 0.02037357 0.02037357]] round 6 [[0.46010028 0.03905229 0.46010028 0.02037357 0.02037357]] round 7 [[0.46010028 0.03905229 0.46010028 0.02037357 0.02037357]]2020-09-26
建强思考题: 我尝试改了一下老师的代码,把迭代结束条件改为计算前后两次PageRank向量的差的平均值是否小于指定精度,发现这个迭代过程收敛很快,只用了7轮循环就结束了,程序部分代码如下,不当之处请老师指正: # 采样迭代方式,判断前后两次PageRank向量的差的平均值是否小于指定精度。 pricision = 1e-9 # 设置计算精度 last_pr = None i = 0 while True: # 进行点乘,计算Σ(PR(pj)/L(pj)) pr = np.dot(pr, adj) # 转置保存Σ(PR(pj)/L(pj))结果的矩阵,并增加长度为N的列向量,其中每个元素的值为1/N,便于下一步的点乘。 pr_jump = np.full([N, 2], [[0, 1/N]]) pr_jump[:,:-1] = pr.transpose() # 进行点乘,计算α(Σ(PR(pj)/L(pj))) + (1-α)/N) pr = np.dot(pr_jump, jump) # 归一化PageRank得分,由于计算后pr是列向量,因此需要做转置 pr = pr.transpose() pr = pr / pr.sum() print("round", i + 1, pr) if last_pr is not None: diff = np.average(np.absolute(pr - last_pr)) if diff <= pricision: break last_pr = pr.copy() i += 1 ############程序输出############# round 1 [[0.37027027 0.24864865 0.37027027 0.00540541 0.00540541]] round 2 [[0.46740902 0.02498642 0.46740902 0.02009777 0.02009777]] round 3 [[0.46023676 0.03878962 0.46023676 0.02036842 0.02036842]] round 4 [[0.46010283 0.03904738 0.46010283 0.02037348 0.02037348]] round 5 [[0.46010033 0.0390522 0.46010033 0.02037357 0.02037357]] round 6 [[0.46010028 0.03905229 0.46010028 0.02037357 0.02037357]] round 7 [[0.46010028 0.03905229 0.46010028 0.02037357 0.02037357]]2020-09-26 郭俊杰#上面的代码中pr变值改为pr_tmp #========================== i = 0 errorRate = 0.000001 while (True): # 进行点乘,计算Σ(PR(pj)/L(pj)) pr = np.dot(pr_tmp, adj) # 转置保存Σ(PR(pj)/L(pj))结果的矩阵,并增加长度为N的列向量,其中每个元素的值为1/N,便于下一步的点乘。 pr_jump = np.full([N, 2], [[0, 1 / N]]) pr_jump[:, :-1] = pr.transpose() # 进行点乘,计算α(Σ(PR(pj)/L(pj))) + (1-α)/N) pr = np.dot(pr_jump, jump) # 归一化PageRank得分 pr = pr.transpose() pr = pr / pr.sum() delta = list(map(abs, (pr/pr_tmp))) delta = abs(np.max(delta)-1) if delta <= errorRate: break else: pr_tmp = pr i += 1 continue print('round:', i) print('pr:', pr)2020-06-041
郭俊杰#上面的代码中pr变值改为pr_tmp #========================== i = 0 errorRate = 0.000001 while (True): # 进行点乘,计算Σ(PR(pj)/L(pj)) pr = np.dot(pr_tmp, adj) # 转置保存Σ(PR(pj)/L(pj))结果的矩阵,并增加长度为N的列向量,其中每个元素的值为1/N,便于下一步的点乘。 pr_jump = np.full([N, 2], [[0, 1 / N]]) pr_jump[:, :-1] = pr.transpose() # 进行点乘,计算α(Σ(PR(pj)/L(pj))) + (1-α)/N) pr = np.dot(pr_jump, jump) # 归一化PageRank得分 pr = pr.transpose() pr = pr / pr.sum() delta = list(map(abs, (pr/pr_tmp))) delta = abs(np.max(delta)-1) if delta <= errorRate: break else: pr_tmp = pr i += 1 continue print('round:', i) print('pr:', pr)2020-06-041
收起评论

