11 | 树的深度优先搜索(上):如何才能高效率地查字典?
黄申

该思维导图由 AI 生成,仅供参考
你好,我是黄申。
你还记得迭代法中的二分查找吗?在那一讲中,我们讨论了一个查字典的例子。如果要使用二分查找,我们首先要把整个字典排个序,然后每次都通过二分的方法来缩小搜索范围。
不过在平时的生活中,咱们查字典并不是这么做的。我们都是从单词的最左边的字母开始,逐个去查找。比如查找“boy”这个单词,我们一般是这么查的。首先,在 a~z 这 26 个英文字母里找到单词的第一个字母 b,然后在 b 开头的单词里找到字母 o,最终在 bo 开头的单词里找到字母 y。
你可以看我画的这种树状图,其实就是从树顶层的根结点一直遍历到最下层的叶子结点,最终逐步构成单词前缀的过程。对应的数据结构就是前缀树(prefix tree),或者叫字典树(trie)。我个人更喜欢前缀树这个名称,因为看到这个名词,这个数据结构的特征就一目了然。
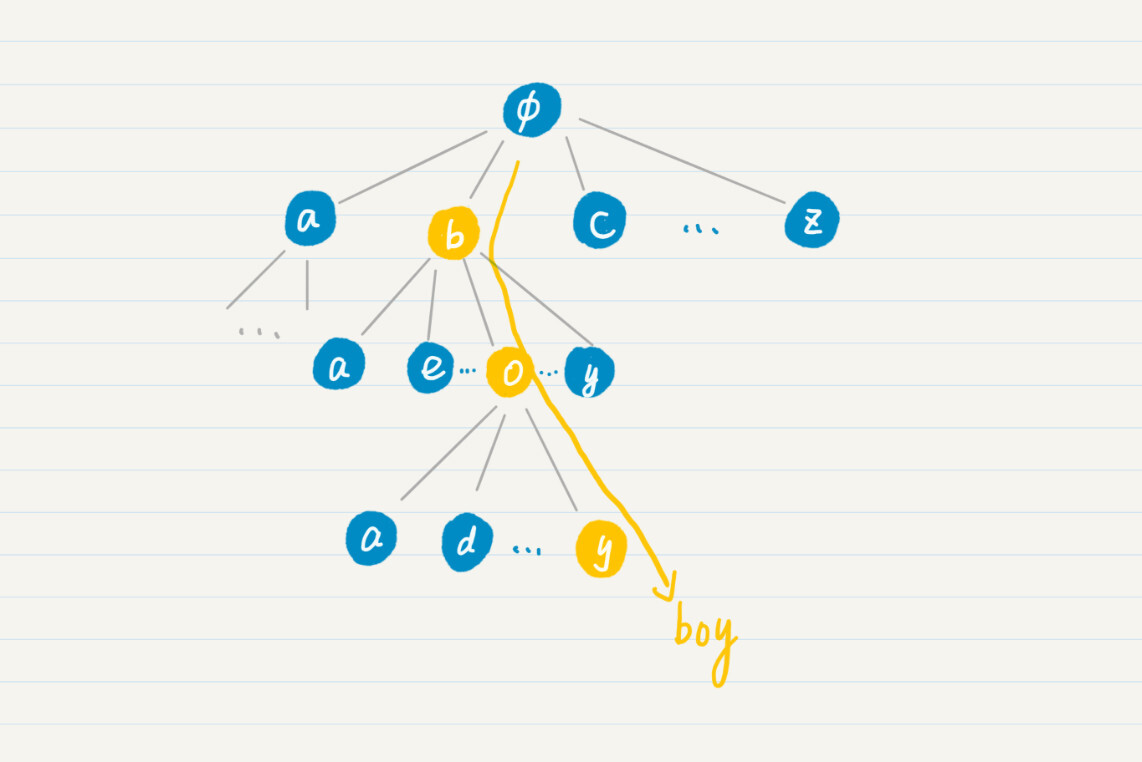
那前缀树究竟该如何构建呢?有了前缀树,我们又该如何查询呢?今天,我会从图论的基本概念出发,来给你讲一下什么样的结构是树,以及如何通过树的深度优先搜索,来实现前缀树的构建和查询。
图论的一些基本概念
前缀树是一种有向树。那什么是有向树?顾名思义,有向树就是一种树,特殊的就是,它的边是有方向的。而树是没有简单回路的连通图。
公开
同步至部落
取消
完成
0/2000
笔记
复制
AI
- 深入了解
- 翻译
- 解释
- 总结

本文深入介绍了有向树和前缀树的构建与查询过程,以及利用深度优先搜索实现快速字典查询的方法。首先从数学中图的基本定义入手,引出了有向树及其在计算机领域的广泛应用。文章详细讲解了前缀树的构建过程,并通过图示和实际例子生动地解释了前缀树的查询过程。此外,还提出了思考题,鼓励读者尝试实现前缀树并分享学习笔记。整体而言,本文内容丰富,深入浅出,适合对树结构和深度优先搜索感兴趣的读者阅读学习。
仅可试看部分内容,如需阅读全部内容,请付费购买文章所属专栏
《程序员的数学基础课》,新⼈⾸单¥68
《程序员的数学基础课》,新⼈⾸单¥68
立即购买
© 版权归极客邦科技所有,未经许可不得传播售卖。 页面已增加防盗追踪,如有侵权极客邦将依法追究其法律责任。
登录 后留言
全部留言(25)
- 最新
- 精选
 Healtheon老师讲解得非常好,谈下个人对前缀树的了解,前缀树主要应用于以下场景: 1.预测文本输入功能:搜索引擎的输入框中输入搜索关键词的预测文本提示、IDE代码编辑器和浏览器网址中输入时的预测文本提示,借助老师讲的前两节动态规划实现预测文本的纠错功能; 2.使用前缀树结构对字符串或单词按字母顺序实现排序并进行输出的功能; 3.前缀树也可用于实现近似匹配,包括拼写检查和连字软件使用的算法; 前缀树的主要优劣对比: 1.使用前缀树可以高效地进行前缀搜索字符串和插入字符串,时间复杂度为O(length); 2.使用前缀树可以按字母顺序轻松打印所有字符串,该功能是散列表不易实现的,但前缀树的搜索效率可能不如散列表快; 3.前缀树的缺点在于,需要大量的内存来存储字符串,对于每个节点需要太多的节点指针。倘若关注内存空间上的优化,可以考虑使用三元搜索树。三元搜索树是实现字典的首选结构,其搜索字符串的时间复杂度是O(height);
Healtheon老师讲解得非常好,谈下个人对前缀树的了解,前缀树主要应用于以下场景: 1.预测文本输入功能:搜索引擎的输入框中输入搜索关键词的预测文本提示、IDE代码编辑器和浏览器网址中输入时的预测文本提示,借助老师讲的前两节动态规划实现预测文本的纠错功能; 2.使用前缀树结构对字符串或单词按字母顺序实现排序并进行输出的功能; 3.前缀树也可用于实现近似匹配,包括拼写检查和连字软件使用的算法; 前缀树的主要优劣对比: 1.使用前缀树可以高效地进行前缀搜索字符串和插入字符串,时间复杂度为O(length); 2.使用前缀树可以按字母顺序轻松打印所有字符串,该功能是散列表不易实现的,但前缀树的搜索效率可能不如散列表快; 3.前缀树的缺点在于,需要大量的内存来存储字符串,对于每个节点需要太多的节点指针。倘若关注内存空间上的优化,可以考虑使用三元搜索树。三元搜索树是实现字典的首选结构,其搜索字符串的时间复杂度是O(height);作者回复: 总结的很好,还有实用的场景
2019-01-07249 Healtheon下面是构建前缀树和查询的代码实现: package com.string.test; /** * Created by hanyonglu on 2019/1/7. */ public class TrieTest { private static final int CHARACTER_SIZE = 26; private TrieNode root; private static class TrieNode { private TrieNode[] children; private boolean isWordEnd; public TrieNode() { isWordEnd = false; children = new TrieNode[CHARACTER_SIZE]; for (int index = 0; index < CHARACTER_SIZE; index++) { children[index] = null; } } } public void insert(String key) { TrieNode newNode = root; int index; for (int i = 0; i < key.length(); i++) { index = key.charAt(i) - 'a'; if (newNode.children[index] == null) { newNode.children[index] = new TrieNode(); } newNode = newNode.children[index]; } newNode.isWordEnd = true; } public boolean search(String key) { TrieNode searchNode = root; int index; for (int i = 0; i < key.length(); i++) { index = key.charAt(i) - 'a'; if (searchNode.children[index] == null) { return false; } searchNode = searchNode.children[index]; } return (searchNode != null && searchNode.isWordEnd); } public static void main(String args[]) { String[] keys = {"my", "name", "is", "hanyonglu", "the", "son", "handongyang", "home", "near", "not", "their"}; TrieTest trieTest = new TrieTest(); trieTest.root = new TrieNode(); for (int index = 0; index < keys.length ; index++) { trieTest.insert(keys[index]); } System.out.println("home result : " + trieTest.search("home")); System.out.println("their result : " + trieTest.search("their")); System.out.println("t result : " + trieTest.search("t")); } }
Healtheon下面是构建前缀树和查询的代码实现: package com.string.test; /** * Created by hanyonglu on 2019/1/7. */ public class TrieTest { private static final int CHARACTER_SIZE = 26; private TrieNode root; private static class TrieNode { private TrieNode[] children; private boolean isWordEnd; public TrieNode() { isWordEnd = false; children = new TrieNode[CHARACTER_SIZE]; for (int index = 0; index < CHARACTER_SIZE; index++) { children[index] = null; } } } public void insert(String key) { TrieNode newNode = root; int index; for (int i = 0; i < key.length(); i++) { index = key.charAt(i) - 'a'; if (newNode.children[index] == null) { newNode.children[index] = new TrieNode(); } newNode = newNode.children[index]; } newNode.isWordEnd = true; } public boolean search(String key) { TrieNode searchNode = root; int index; for (int i = 0; i < key.length(); i++) { index = key.charAt(i) - 'a'; if (searchNode.children[index] == null) { return false; } searchNode = searchNode.children[index]; } return (searchNode != null && searchNode.isWordEnd); } public static void main(String args[]) { String[] keys = {"my", "name", "is", "hanyonglu", "the", "son", "handongyang", "home", "near", "not", "their"}; TrieTest trieTest = new TrieTest(); trieTest.root = new TrieNode(); for (int index = 0; index < keys.length ; index++) { trieTest.insert(keys[index]); } System.out.println("home result : " + trieTest.search("home")); System.out.println("their result : " + trieTest.search("their")); System.out.println("t result : " + trieTest.search("t")); } }作者回复: 实现很简洁👍
2019-01-0725 Being关于思考题的一点想法:其实可以将单词以及字母抽象出来,利用组合模式,形成树形关系,实现递归调用。
Being关于思考题的一点想法:其实可以将单词以及字母抽象出来,利用组合模式,形成树形关系,实现递归调用。作者回复: 如果使用前缀树,对给定的一些单词进行处理,就无需排列组合了
2019-01-075- 梦倚栏杆对于二叉树而言,深度优先遍历是不是就是二叉树的先序遍历啊
作者回复: 确切的说,先序、中序和后序是深度优先遍历的三种方式
2019-03-263  Cutler正好最近刷到了leetcode上一道关于trie树的题 ## Algorithm ### 1. 题目 ``` 208. 实现 Trie (前缀树) ``` ### 2. 题目描述 ``` 实现一个 Trie (前缀树),包含 insert, search, 和 startsWith 这三个操作。 示例: Trie trie = new Trie(); trie.insert("apple"); trie.search("apple"); // 返回 true trie.search("app"); // 返回 false trie.startsWith("app"); // 返回 true trie.insert("app"); trie.search("app"); // 返回 true 说明: 你可以假设所有的输入都是由小写字母 a-z 构成的。 保证所有输入均为非空字符串。 ``` ### 3. 解答: ```golang type Trie struct { data byte child []*Trie isEnd bool } /** Initialize your data structure here. */ func Constructor() Trie { return Trie{ data: '/', child: make([]*Trie, 26, 26), isEnd: false, } } func newTrie(data byte) *Trie { return &Trie{ data: data, child: make([]*Trie, 26, 26), } } /** Inserts a word into the trie. */ func (t *Trie) Insert(word string) { p := t for _, c := range word { index := c - 'a' if p.child[index] == nil { p.child[index] = newTrie(byte(c)) } p = p.child[index] } p.isEnd = true } /** Returns if the word is in the trie. */ func (t *Trie) Search(word string) bool { p := t for _, c := range word { index := c - 'a' if p.child[index] == nil { return false } p = p.child[index] } if !p.isEnd { return false } else { return true } } /** Returns if there is any word in the trie that starts with the given prefix. */ func (t *Trie) StartsWith(prefix string) bool { p := t for _, c := range prefix { index := c - 'a' if p.child[index] == nil { return false } p = p.child[index] } return true } ``` ### 4. 说明 1. 定义Trie的结构中包含的child 2. child数组用26个英文字符表示,用字符减去`a`就得到数组中的索引
Cutler正好最近刷到了leetcode上一道关于trie树的题 ## Algorithm ### 1. 题目 ``` 208. 实现 Trie (前缀树) ``` ### 2. 题目描述 ``` 实现一个 Trie (前缀树),包含 insert, search, 和 startsWith 这三个操作。 示例: Trie trie = new Trie(); trie.insert("apple"); trie.search("apple"); // 返回 true trie.search("app"); // 返回 false trie.startsWith("app"); // 返回 true trie.insert("app"); trie.search("app"); // 返回 true 说明: 你可以假设所有的输入都是由小写字母 a-z 构成的。 保证所有输入均为非空字符串。 ``` ### 3. 解答: ```golang type Trie struct { data byte child []*Trie isEnd bool } /** Initialize your data structure here. */ func Constructor() Trie { return Trie{ data: '/', child: make([]*Trie, 26, 26), isEnd: false, } } func newTrie(data byte) *Trie { return &Trie{ data: data, child: make([]*Trie, 26, 26), } } /** Inserts a word into the trie. */ func (t *Trie) Insert(word string) { p := t for _, c := range word { index := c - 'a' if p.child[index] == nil { p.child[index] = newTrie(byte(c)) } p = p.child[index] } p.isEnd = true } /** Returns if the word is in the trie. */ func (t *Trie) Search(word string) bool { p := t for _, c := range word { index := c - 'a' if p.child[index] == nil { return false } p = p.child[index] } if !p.isEnd { return false } else { return true } } /** Returns if there is any word in the trie that starts with the given prefix. */ func (t *Trie) StartsWith(prefix string) bool { p := t for _, c := range prefix { index := c - 'a' if p.child[index] == nil { return false } p = p.child[index] } return true } ``` ### 4. 说明 1. 定义Trie的结构中包含的child 2. child数组用26个英文字符表示,用字符减去`a`就得到数组中的索引作者回复: Leetcode是不错的编程训练资源
2020-11-071 是我觉得二叉树跟正则表达式好像
是我觉得二叉树跟正则表达式好像作者回复: 具体是哪种正则表达式?
2019-05-1621 崔晓乐这里的简单回路,其实就是指,除了第一个结点和最后一个结点相同外,其余结点不重复出现的回路? 这句话怎么理解呢? 其余结点不重复出现的回路?
崔晓乐这里的简单回路,其实就是指,除了第一个结点和最后一个结点相同外,其余结点不重复出现的回路? 这句话怎么理解呢? 其余结点不重复出现的回路?作者回复: 就是说只有第一个结点和最后一个结点重复出现。而其他的所有结点都只出现一次
2021-09-14 张祈璟把词都放在个数据库里,查询的时候用like,与把词放树里的效率哪个高?实现起来哪个简单?
张祈璟把词都放在个数据库里,查询的时候用like,与把词放树里的效率哪个高?实现起来哪个简单?作者回复: 数据库的like应该是模糊匹配,通常情况下没有字典树精确匹配的效率高
2021-06-10 北极的大企鹅讲得非常好
北极的大企鹅讲得非常好作者回复: 很高兴对你有价值
2021-04-12 aoe这次通俗易懂,感谢老师
aoe这次通俗易懂,感谢老师作者回复: 很高兴对你有价值
2019-12-02
收起评论

