14 | 乘法器:如何像搭乐高一样搭电路(下)?

该思维导图由 AI 生成,仅供参考
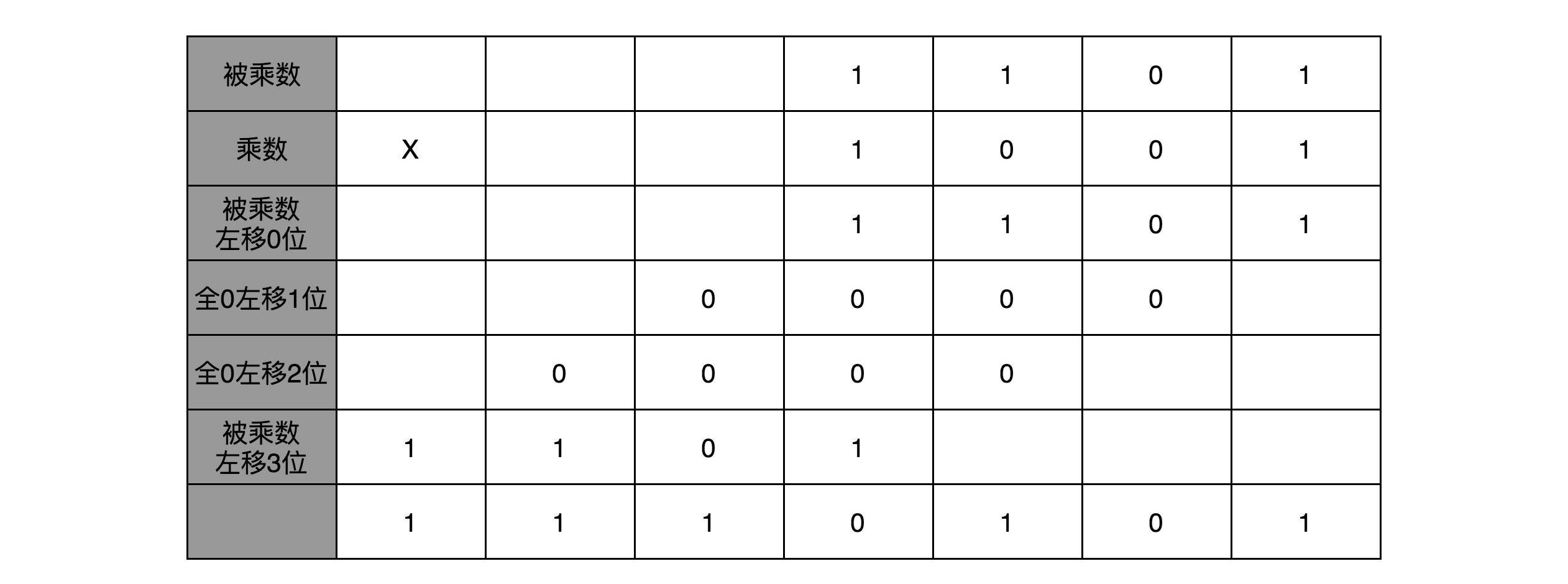
顺序乘法的实现过程
- 深入了解
- 翻译
- 解释
- 总结

本文介绍了乘法器的基本原理和优化方法。通过将乘法转化为加法和位移的操作,可以用简单的电路实现乘法运算。文章指出,顺序乘法器虽然简单,但计算速度较慢,时间复杂度为O(N),需要进行多次加法操作。为了提高计算速度,可以采用并行加速方法,将多个加法操作同时进行,从而降低时间复杂度至O(logN)。然而,并行加速方法需要更多的硬件资源来存储中间计算结果。文章还讨论了电路的并行性和门延迟的问题,以及硬件电路设计中的权衡。通过精巧地设计电路,可以用较少的门电路和寄存器完成复杂的乘法运算。最后,文章提到了计算机体系结构中RISC和CISC的经典历史路线之争,以及对读者的推荐阅读和课后思考。整体而言,本文深入浅出地介绍了乘法器的实现原理和相关技术细节,对于对计算机硬件感兴趣的读者具有很高的参考价值。
《深入浅出计算机组成原理》,新⼈⾸单¥68
全部留言(51)
- 最新
- 精选
 奕最后一个的展开电路图,没有看懂
奕最后一个的展开电路图,没有看懂编辑回复: 这里想要解决的问题是,如果电路的“层数”太深,意味着一次运算需要的时钟循环数会太多,这样CPU就会“慢”,所以我们就把原先的电路尽量展开到比较少的层数,虽然这可能意味着电路的晶体管数量的增加。 具体到这里的加法,是把两个4位的二进制数相加,一个数A,从高位到低位是 A3A2A1A0,第二个数B,从高位到低位是 B3B2B1B0 我们加完之后的和,应该是 C4C3C2C1C0,变成5位,最高位的C4是代表这两个数相加之后是否会溢出一位需要进位。 不展开的情况下,我们计算C4,需要先算出A0和B0的和,以及是否进位,然后把是否进位,再和A1和B1相加,在看是否进位,这样一层层上来,这样的话,整个计算就需要至少5层(现在图里的是3层) 但是实际上我们可以把整个电路图展开,C4这个进位,只有这几种情况: 1. A3+B3 需要进位(两个都是1) 2. A3+B3是1(通过一个一个异或门)并且 A2+B2 进位。这里前面的这个就是图里第二列第一行的P3,后面是同一个节点里面的G2 3. A3+B3是1,并且 A2+B2 是1,并且 A1+B1进位。对应的就是第二列第二行的 P3,P2,G1 4. A3+B3是1,并且 A2+B2 是1,并且 A1+B1是1,并且A0+B0进位。对应的就是第二列第三行的 P3,P2,P1,G1 5. A3+B3是1,并且 A2+B2 是1,并且 A1+B1是1,并且A0+B0是1,并且下面进位上来的标志C0是1,对应的就是第二列第四行的P3,P2,P1,P0,C0 这5个结果就是图里面的第二列的电路,都是与门。然后任意一个条件满足,C4就需要进位,所以C4是这五个 与门 并联之后的 或门。
2019-06-021188 旺旺从加法到乘法,先是计算过程变得复杂了,步骤变得更多,可以像人一样,逐位计算,但线性带来时间复杂度高。从而可以考虑通过增加线路/硬件复杂度,从空间换时间的思路,加快乘法速度。 空间 vs 时间。 但CPU毕竟也是很珍贵的资源,晶体管也不宜太多,这中间需要相互平衡。
旺旺从加法到乘法,先是计算过程变得复杂了,步骤变得更多,可以像人一样,逐位计算,但线性带来时间复杂度高。从而可以考虑通过增加线路/硬件复杂度,从空间换时间的思路,加快乘法速度。 空间 vs 时间。 但CPU毕竟也是很珍贵的资源,晶体管也不宜太多,这中间需要相互平衡。作者回复: 总结得很好,其实这也可以认为是CISC和RISC的路线之争最朴素的由来
2019-05-27238 活的潇洒“这之间的权衡,其实就是计算机体系结构中的RISC和CISC的经典历史路线之争” 这句才是重点,day14 笔记:https://www.cnblogs.com/luoahong/p/10929985.html
活的潇洒“这之间的权衡,其实就是计算机体系结构中的RISC和CISC的经典历史路线之争” 这句才是重点,day14 笔记:https://www.cnblogs.com/luoahong/p/10929985.html作者回复: 👍
2019-05-27314 WB最后一张图片中的加法器是一个与门和一个或门?? 加法器不是由一个与门和一个异或门组成的吗?
WB最后一张图片中的加法器是一个与门和一个或门?? 加法器不是由一个与门和一个异或门组成的吗?作者回复: WB同学你好, 最后一张图是表示如果我们不希望有太多的门延迟的情况下,我们怎么让加法器里面高位的是否获得进位,不用等待前面低位的全加器的计算结果。而不是一个完整的加法器。 我们重新复习一下 13 和 14 两讲的内容 完整的加法器可以由很多个全加器串联起来 全加器由两个半加器外加一个或门组成 半加器由一个与门和一个异或门组成 半加器只是整个加法器中最基础的一个零件
2019-05-2712 愤怒的虾干老师好,最近在看您推荐的计算机组成公开课,x86保护模式下会使用全局符号描述表寻址,同时操作系统又是使用页表来分配地址、映射物理和逻辑地址。我想问全局符号描述表和页表在寻址上有什么区别与联系?
愤怒的虾干老师好,最近在看您推荐的计算机组成公开课,x86保护模式下会使用全局符号描述表寻址,同时操作系统又是使用页表来分配地址、映射物理和逻辑地址。我想问全局符号描述表和页表在寻址上有什么区别与联系?作者回复: 全局符号表是虚拟内存内的内存寻址和跳转。 页表是虚拟内存和物理内存之间的映射关系。
2019-05-275 Become a architect我想现在并发编程的思想起源于此吧。效率确实高了,但是编程的复杂度变高了。
Become a architect我想现在并发编程的思想起源于此吧。效率确实高了,但是编程的复杂度变高了。作者回复: Become a architect同学, 你好,并发的思路是一个很直观的思路,并不是发源于乘法器,反而是乘法器设计的时候,可以去想想并发的思路。 而且这里最后的乘法器,前后的计算其实有依赖关系,我们只是通过分析电路,让部分前后的计算依赖关系解耦合,通过一个更复杂的电路来实现。
2019-12-182 木心4位加法器的最大门延迟是进位,是2*4+1 9个门延迟
木心4位加法器的最大门延迟是进位,是2*4+1 9个门延迟作者回复: 木心同学, 你好,这是一个问题么?电路并行这部分我已经写了,可以做到没有那么多门延迟的。
2019-09-2722 J.D.Chi“把结果加到刚才的结果上”,想起了编程语言里的 sum = sum + i 之类的语句。
J.D.Chi“把结果加到刚才的结果上”,想起了编程语言里的 sum = sum + i 之类的语句。作者回复: J.D.同学, 你好,是很像的
2019-09-212 小广徐老师你好,最后那个展开图,第二列的最下面一个运算组件,标注的表达式是"P3*P2*P1*P0*G0",但是我认为这里是笔误,应该是"P3*P2*P1*P0*C0",应该把G0改为C0,^_^
小广徐老师你好,最后那个展开图,第二列的最下面一个运算组件,标注的表达式是"P3*P2*P1*P0*G0",但是我认为这里是笔误,应该是"P3*P2*P1*P0*C0",应该把G0改为C0,^_^作者回复: 小广同学, 你好,谢谢你,的确是笔误了,应该是C0
2019-09-16 DylanCPU做除法时和做乘法时是相反的,乘法是右移,除法是左移,乘法做的是加法,除法做的是减法。除数右移,商左移,商左移后最右位补0还是1取决于,本次余数和除数相减后余数最高位,最高位1则,回退;0那么商左移后最右位补1。2020-02-25115
DylanCPU做除法时和做乘法时是相反的,乘法是右移,除法是左移,乘法做的是加法,除法做的是减法。除数右移,商左移,商左移后最右位补0还是1取决于,本次余数和除数相减后余数最高位,最高位1则,回退;0那么商左移后最右位补1。2020-02-25115

