43 | 拓扑排序:如何确定代码源文件的编译依赖关系?
王争

该思维导图由 AI 生成,仅供参考
从今天开始,我们就进入了专栏的高级篇。相对基础篇,高级篇涉及的知识点,都比较零散,不是太系统。所以,我会围绕一个实际软件开发的问题,在阐述具体解决方法的过程中,将涉及的知识点给你详细讲解出来。
所以,相较于基础篇“开篇问题 - 知识讲解 - 回答开篇 - 总结 - 课后思考”这样的文章结构,高级篇我稍作了些改变,大致分为这样几个部分:“问题阐述 - 算法解析 - 总结引申 - 课后思考”。
好了,现在,我们就进入高级篇的第一节,如何确定代码源文件的编译依赖关系?
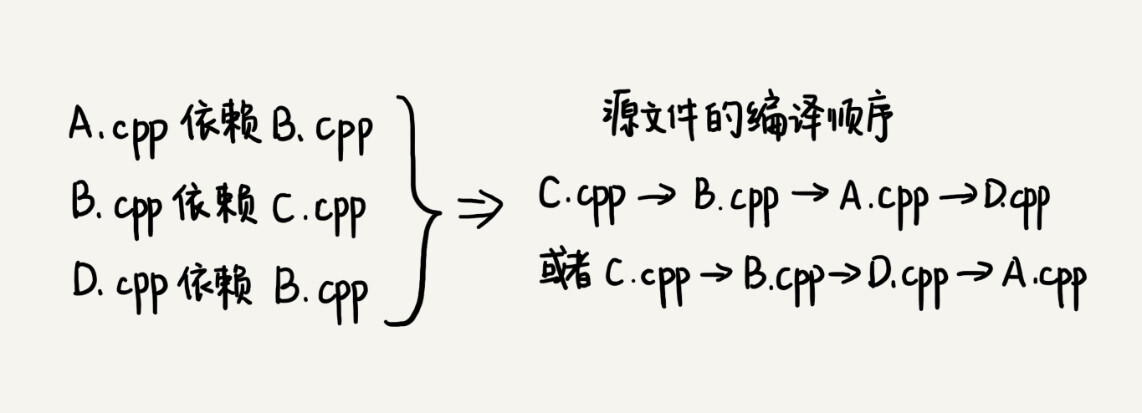
我们知道,一个完整的项目往往会包含很多代码源文件。编译器在编译整个项目的时候,需要按照依赖关系,依次编译每个源文件。比如,A.cpp 依赖 B.cpp,那在编译的时候,编译器需要先编译 B.cpp,才能编译 A.cpp。
编译器通过分析源文件或者程序员事先写好的编译配置文件(比如 Makefile 文件),来获取这种局部的依赖关系。那编译器又该如何通过源文件两两之间的局部依赖关系,确定一个全局的编译顺序呢?
算法解析
这个问题的解决思路与“图”这种数据结构的一个经典算法“拓扑排序算法”有关。那什么是拓扑排序呢?这个概念很好理解,我们先来看一个生活中的拓扑排序的例子。
我们在穿衣服的时候都有一定的顺序,我们可以把这种顺序想成,衣服与衣服之间有一定的依赖关系。比如说,你必须先穿袜子才能穿鞋,先穿内裤才能穿秋裤。假设我们现在有八件衣服要穿,它们之间的两两依赖关系我们已经很清楚了,那如何安排一个穿衣序列,能够满足所有的两两之间的依赖关系?
公开
同步至部落
取消
完成
0/2000
笔记
复制
AI
- 深入了解
- 翻译
- 解释
- 总结

拓扑排序算法在确定代码源文件编译依赖关系中发挥着重要作用。本文首先通过生活中的例子解释了拓扑排序的原理,然后详细介绍了Kahn算法和DFS算法的实现方法。Kahn算法利用贪心算法思想,通过统计入度为0的顶点来实现拓扑排序;而DFS算法则通过深度优先遍历图来实现拓扑排序。此外,文章还指出了拓扑排序的时间复杂度,并探讨了拓扑排序在解决环存在检测问题中的应用。文章最后提出了两个课后思考问题,引发读者深入思考。总的来说,本文通过生动的例子和具体的代码实现,深入浅出地介绍了拓扑排序算法及其在确定代码编译依赖关系中的应用。
仅可试看部分内容,如需阅读全部内容,请付费购买文章所属专栏
《数据结构与算法之美》,新⼈⾸单¥68
《数据结构与算法之美》,新⼈⾸单¥68
立即购买
© 版权归极客邦科技所有,未经许可不得传播售卖。 页面已增加防盗追踪,如有侵权极客邦将依法追究其法律责任。
登录 后留言
全部留言(79)
- 最新
- 精选
 Jerry银银老师,这门专栏快结束了,突然有点新的想法:如果老师在讲解算法的时候,多讲点算法的由来,也就是背景,那就更好了。 我想,如果能知道某个算法的创造者为什么会发明某个算法,怎么能够发明出某个算法,我想我们会掌握得更牢,学得应该也稍微轻松一点,关键是能跟随发明者回到原点,体会思考的过程
Jerry银银老师,这门专栏快结束了,突然有点新的想法:如果老师在讲解算法的时候,多讲点算法的由来,也就是背景,那就更好了。 我想,如果能知道某个算法的创造者为什么会发明某个算法,怎么能够发明出某个算法,我想我们会掌握得更牢,学得应该也稍微轻松一点,关键是能跟随发明者回到原点,体会思考的过程编辑回复: 这个有意思,我们想想。
2019-01-049164 Edward老师你好。我在做一道动态规划题的时候,不借助其他启发性线索时,在纸上演算一遍后,发现自己如果不能直觉地从演算中推演出解答的关键,就会产生强烈的自我怀疑。会有一层对自己智力水平的怀疑,如果没有一定的智商,是不适合做这事情的。请问老师你有什么方法,可以克服这种自我的质疑?
Edward老师你好。我在做一道动态规划题的时候,不借助其他启发性线索时,在纸上演算一遍后,发现自己如果不能直觉地从演算中推演出解答的关键,就会产生强烈的自我怀疑。会有一层对自己智力水平的怀疑,如果没有一定的智商,是不适合做这事情的。请问老师你有什么方法,可以克服这种自我的质疑?作者回复: 多练习 多思考 多总结 慢慢就好了 都有这么一个过程的
2019-01-05416 欢乐小熊老师, 专栏一直跟进到现在了, 每堂课都是对知识的巩固和完善, 额...不过我一直有个小问题想请教一下老师, 那就是老师的图是使用什么工具绘制的, 我觉得非常富有生命力, 记录在笔记里非常 nice ...
欢乐小熊老师, 专栏一直跟进到现在了, 每堂课都是对知识的巩固和完善, 额...不过我一直有个小问题想请教一下老师, 那就是老师的图是使用什么工具绘制的, 我觉得非常富有生命力, 记录在笔记里非常 nice ...编辑回复: iPad Paper
2019-01-046 NeverMore1、反过来的话计算的就不是入度了,可以用出度来判断; 2、BFS的话,则需要记录上一个节点是哪个,可以实现,但是比DFS要麻烦些。 还请老师指点。 老师之后能不能给思考题一个答疑?
NeverMore1、反过来的话计算的就不是入度了,可以用出度来判断; 2、BFS的话,则需要记录上一个节点是哪个,可以实现,但是比DFS要麻烦些。 还请老师指点。 老师之后能不能给思考题一个答疑?作者回复: 专栏结束的时候吧 也算是一个回顾 现在年底忙 没啥时间写呢
2019-01-044- Geek_18b741DFS 算法的时间复杂度计算中,为什么每个顶点访问两次?每个顶点进入dfs是一次呀?
作者回复: dfs是栈的思想,一进一出就被访问了两次
2019-10-241  djfhchdh请教个问题,思考题2是否可以基于Kahn算法,稍微改造一下,成为一个BFS的实现?即从入度为0的顶点开始,逐层遍历。。。
djfhchdh请教个问题,思考题2是否可以基于Kahn算法,稍微改造一下,成为一个BFS的实现?即从入度为0的顶点开始,逐层遍历。。。作者回复: 不是逐层遍历,逐层不行的
2019-05-29 不系之舟老师您好,还看到过另一个深度优先遍历的方法,是通过将节点涂不同的颜色判断是否在遍历的时候遇到了环,这种方法看着应该很明了,但是好像很少看到有人这么写程序,不知道是什么原因呢?
不系之舟老师您好,还看到过另一个深度优先遍历的方法,是通过将节点涂不同的颜色判断是否在遍历的时候遇到了环,这种方法看着应该很明了,但是好像很少看到有人这么写程序,不知道是什么原因呢?作者回复: 那个比较大而全,所以不经常用。
2019-01-19 Alexis何春光kahn算法中统计每个顶点的入度,有两层循环,时间复杂度为什么不是O(V*E)呢?
Alexis何春光kahn算法中统计每个顶点的入度,有两层循环,时间复杂度为什么不是O(V*E)呢?作者回复: 第一层是v 但第二层不是E呢
2019-01-132 往事随风,顺其自然public void topoSortByDFS() { // 先构建逆邻接表,边 s->t 表示,s 依赖于 t,t 先于 s LinkedList<Integer> inverseAdj[] = new LinkedList[v]; for (int i = 0; i < v; ++i) { // 申请空间 inverseAdj[i] = new LinkedList<>(); } for (int i = 0; i < v; ++i) { // 通过邻接表生成逆邻接表 for (int j = 0; j < adj[i].size(); ++j) { int w = adj[i].get(j); // i->w inverseAdj[w].add(i); // w->i } } boolean[] visited = new boolean[v]; for (int i = 0; i < v; ++i) { // 深度优先遍历图 if (visited[i] == false) { visited[i] = true; dfs(i, inverseAdj, visited); } } } private void dfs( int vertex, LinkedList<Integer> inverseAdj[], boolean[] visited) { for (int i = 0; i < inverseAdj[vertex].size(); ++i) { int w = inverseAdj[vertex].get(i); if (visited[w] == true) continue; visited[w] = true; dfs(w, inverseAdj, visited); } // 先把 vertex 这个顶点可达的所有顶点都打印出来之后,再打印它自己 System.out.print("->" + vertex); } // int w = adj[i].get(j); // i->w 这个W表示什么? inverseAdj[w].add(i); // w->i 为啥是相反的邻接?这个不也是从0-i来存对应的值?
往事随风,顺其自然public void topoSortByDFS() { // 先构建逆邻接表,边 s->t 表示,s 依赖于 t,t 先于 s LinkedList<Integer> inverseAdj[] = new LinkedList[v]; for (int i = 0; i < v; ++i) { // 申请空间 inverseAdj[i] = new LinkedList<>(); } for (int i = 0; i < v; ++i) { // 通过邻接表生成逆邻接表 for (int j = 0; j < adj[i].size(); ++j) { int w = adj[i].get(j); // i->w inverseAdj[w].add(i); // w->i } } boolean[] visited = new boolean[v]; for (int i = 0; i < v; ++i) { // 深度优先遍历图 if (visited[i] == false) { visited[i] = true; dfs(i, inverseAdj, visited); } } } private void dfs( int vertex, LinkedList<Integer> inverseAdj[], boolean[] visited) { for (int i = 0; i < inverseAdj[vertex].size(); ++i) { int w = inverseAdj[vertex].get(i); if (visited[w] == true) continue; visited[w] = true; dfs(w, inverseAdj, visited); } // 先把 vertex 这个顶点可达的所有顶点都打印出来之后,再打印它自己 System.out.print("->" + vertex); } // int w = adj[i].get(j); // i->w 这个W表示什么? inverseAdj[w].add(i); // w->i 为啥是相反的邻接?这个不也是从0-i来存对应的值?作者回复: i-》w表示存在一条顶点i到顶点w的有向边
2019-01-05 往事随风,顺其自然public void topoSortByKahn() { for (int i = 0; i < v; ++i) {// for (int j = 0; j < adj[i].size(); ++j) { int w = adj[i].get(j); // i->w } } 为什么要用两层循环遍历,不是直接遍历链表旧可以?
往事随风,顺其自然public void topoSortByKahn() { for (int i = 0; i < v; ++i) {// for (int j = 0; j < adj[i].size(); ++j) { int w = adj[i].get(j); // i->w } } 为什么要用两层循环遍历,不是直接遍历链表旧可以?作者回复: 遍历每个顶点的链表 每个顶点的链表是独立存储的
2019-01-05
收起评论

