12 | 排序(下):如何用快排思想在O(n)内查找第K大元素?
王争

该思维导图由 AI 生成,仅供参考
上一节我讲了冒泡排序、插入排序、选择排序这三种排序算法,它们的时间复杂度都是 O(n2),比较高,适合小规模数据的排序。今天,我讲两种时间复杂度为 O(nlogn) 的排序算法,归并排序和快速排序。这两种排序算法适合大规模的数据排序,比上一节讲的那三种排序算法要更常用。
归并排序和快速排序都用到了分治思想,非常巧妙。我们可以借鉴这个思想,来解决非排序的问题,比如:如何在 O(n) 的时间复杂度内查找一个无序数组中的第 K 大元素? 这就要用到我们今天要讲的内容。
归并排序的原理
我们先来看归并排序(Merge Sort)。
归并排序的核心思想还是蛮简单的。如果要排序一个数组,我们先把数组从中间分成前后两部分,然后对前后两部分分别排序,再将排好序的两部分合并在一起,这样整个数组就都有序了。
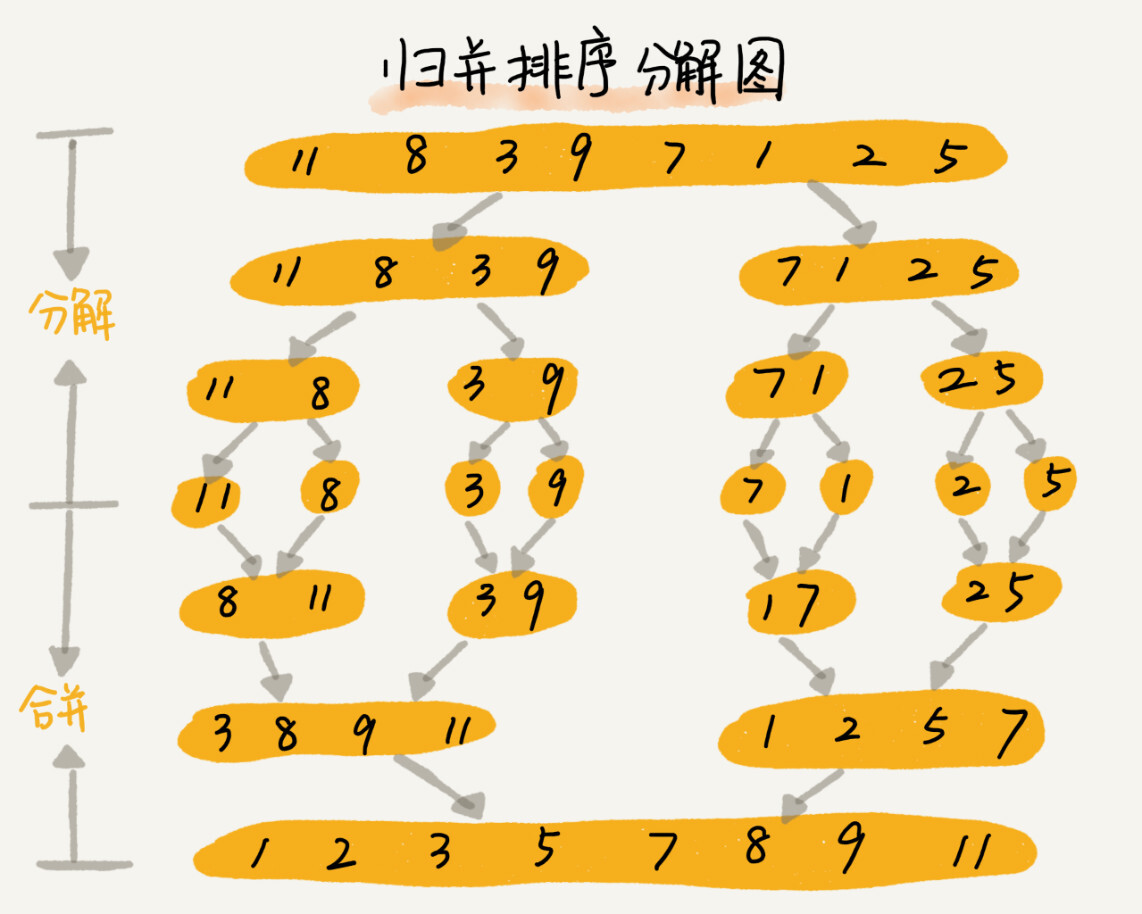
归并排序使用的就是分治思想。分治,顾名思义,就是分而治之,将一个大问题分解成小的子问题来解决。小的子问题解决了,大问题也就解决了。
从我刚才的描述,你有没有感觉到,分治思想跟我们前面讲的递归思想很像。是的,分治算法一般都是用递归来实现的。分治是一种解决问题的处理思想,递归是一种编程技巧,这两者并不冲突。分治算法的思想我后面会有专门的一节来讲,现在不展开讨论,我们今天的重点还是排序算法。
公开
同步至部落
取消
完成
0/2000
笔记
复制
AI
- 深入了解
- 翻译
- 解释
- 总结

归并排序和快速排序是两种常见的排序算法,它们都利用了分治思想,通过递归实现排序。归并排序的时间复杂度为O(nlogn),但不是原地排序算法;而快速排序也是O(nlogn),并且通过巧妙的原地分区函数实现原地排序,但在最坏情况下可能退化为O(n^2)的时间复杂度。归并排序稳定但非原地排序,而快速排序是原地排序但不稳定。读者通过本文可以快速了解这两种排序算法的原理、性能特点以及适用场景,为进一步深入学习和应用排序算法提供了重要参考。此外,文章还提到了快速排序的核心思想和时间复杂度分析,以及在处理大规模日志文件合并时的解决思路。整体而言,本文内容涵盖了排序算法的基本原理和实际应用,对读者具有较高的参考价值。
仅可试看部分内容,如需阅读全部内容,请付费购买文章所属专栏
《数据结构与算法之美》,新⼈⾸单¥68
《数据结构与算法之美》,新⼈⾸单¥68
立即购买
© 版权归极客邦科技所有,未经许可不得传播售卖。 页面已增加防盗追踪,如有侵权极客邦将依法追究其法律责任。
登录 后留言
全部留言(702)
- 最新
- 精选
 峰置顶每次从各个文件中取一条数据,在内存中根据数据时间戳构建一个最小堆,然后每次把最小值给写入新文件,同时将最小值来自的那个文件再出来一个数据,加入到最小堆中。这个空间复杂度为常数,但没能很好利用1g内存,而且磁盘单个读取比较慢,所以考虑每次读取一批数据,没了再从磁盘中取,时间复杂度还是一样O(n)。2018-10-1712330
峰置顶每次从各个文件中取一条数据,在内存中根据数据时间戳构建一个最小堆,然后每次把最小值给写入新文件,同时将最小值来自的那个文件再出来一个数据,加入到最小堆中。这个空间复杂度为常数,但没能很好利用1g内存,而且磁盘单个读取比较慢,所以考虑每次读取一批数据,没了再从磁盘中取,时间复杂度还是一样O(n)。2018-10-1712330 Light Lin伪代码反而看得费劲,可能还是对代码不够敏感吧
Light Lin伪代码反而看得费劲,可能还是对代码不够敏感吧作者回复: 那我以后还是写代码吧
2018-10-1724578 李建辉先构建十条io流,分别指向十个文件,每条io流读取对应文件的第一条数据,然后比较时间戳,选择出时间戳最小的那条数据,将其写入一个新的文件,然后指向该时间戳的io流读取下一行数据,然后继续刚才的操作,比较选出最小的时间戳数据,写入新文件,io流读取下一行数据,以此类推,完成文件的合并, 这种处理方式,日志文件有n个数据就要比较n次,每次比较选出一条数据来写入,时间复杂度是O(n),空间复杂度是O(1),几乎不占用内存,这是我想出的认为最好的操作了,希望老师指出最佳的做法!!!
李建辉先构建十条io流,分别指向十个文件,每条io流读取对应文件的第一条数据,然后比较时间戳,选择出时间戳最小的那条数据,将其写入一个新的文件,然后指向该时间戳的io流读取下一行数据,然后继续刚才的操作,比较选出最小的时间戳数据,写入新文件,io流读取下一行数据,以此类推,完成文件的合并, 这种处理方式,日志文件有n个数据就要比较n次,每次比较选出一条数据来写入,时间复杂度是O(n),空间复杂度是O(1),几乎不占用内存,这是我想出的认为最好的操作了,希望老师指出最佳的做法!!!作者回复: 你回答的不错 思路是正确的
2018-10-2860507 sherry还是觉得伪代码更好,理解思路然后可以写成自己写练练手,看完代码后就没啥想写的欲望了。
sherry还是觉得伪代码更好,理解思路然后可以写成自己写练练手,看完代码后就没啥想写的欲望了。作者回复: 真是众口难调啊😢
2018-10-21883 大汉我是一个笨的人,一节课要看很多遍,但是我知道,只要比聪明的人多看几遍,就也会达到同样的效果
大汉我是一个笨的人,一节课要看很多遍,但是我知道,只要比聪明的人多看几遍,就也会达到同样的效果作者回复: 👍,加油💪
2019-10-17969 斗米担米当 T(n/2^k)=T(1) 时,也就是 n/2^k=1 这个为什么会等于T(1)啊
斗米担米当 T(n/2^k)=T(1) 时,也就是 n/2^k=1 这个为什么会等于T(1)啊作者回复: 最后数据区间变成1的时候排序就完成了 我们看n经过了多少次分解会变成1
2018-11-05343
 angel😇txy🤓大家都说快排的伪代码不好理解,我用JAVA翻译了一下,实测通过,老师给个置顶哈。private static void quickSortC(int[] a, int p, int r) { if (p >= r) { return; } int q = partition(a, p, r); quickSortC(a, p, q - 1); quickSortC(a, q + 1, r); } public static int partition(int[] a, int start, int end) { int pivot = a[end]; int i = start; for (int j = start; j < end; j++) { if (a[j] < pivot) { swap(a, i, j); i = i + 1; } } swap(a, i, end); return i; }
angel😇txy🤓大家都说快排的伪代码不好理解,我用JAVA翻译了一下,实测通过,老师给个置顶哈。private static void quickSortC(int[] a, int p, int r) { if (p >= r) { return; } int q = partition(a, p, r); quickSortC(a, p, q - 1); quickSortC(a, q + 1, r); } public static int partition(int[] a, int start, int end) { int pivot = a[end]; int i = start; for (int j = start; j < end; j++) { if (a[j] < pivot) { swap(a, i, j); i = i + 1; } } swap(a, i, end); return i; }作者回复: 👍
2019-08-28629 刘远通老师 这个地方我没看懂... “第一次分区查找,我们需要对大小为 n 的数组执行分区操作,需要遍历 n 个元素。第二次分区查找,我们只需要对大小为 n/2 的数组执行分区操作,需要遍历 n/2 个元素。依次类推,分区遍历元素的个数分别为、n/2、n/4、n/8、n/16.……直到区间缩小为 1。” 这里讨论的是最平均的情况吗? 最坏的情况可以n,n-1,...,1啊
刘远通老师 这个地方我没看懂... “第一次分区查找,我们需要对大小为 n 的数组执行分区操作,需要遍历 n 个元素。第二次分区查找,我们只需要对大小为 n/2 的数组执行分区操作,需要遍历 n/2 个元素。依次类推,分区遍历元素的个数分别为、n/2、n/4、n/8、n/16.……直到区间缩小为 1。” 这里讨论的是最平均的情况吗? 最坏的情况可以n,n-1,...,1啊作者回复: 平均。你说的没错。最坏情况是你说的那样
2018-10-1717 xr你可能会说,我有个很笨的办法,每次取数组中的最小值,将其移动到数组的最前面,然后在剩下的数组中继续找最小值,以此类推,执行 K 次,找到的数据不就是第 K 大元素了吗? 应该是每次取数组中的最“大”值放到前面吧,因为找的是第k大元素?
xr你可能会说,我有个很笨的办法,每次取数组中的最小值,将其移动到数组的最前面,然后在剩下的数组中继续找最小值,以此类推,执行 K 次,找到的数据不就是第 K 大元素了吗? 应该是每次取数组中的最“大”值放到前面吧,因为找的是第k大元素?作者回复: 嗯嗯 感谢指出
2018-11-14314 趁风卷快排的partition函数的空间复杂度是O(1),但整个排序过程是递归的,最多会有O(logn)个函数放在栈里。这一部分不算空间复杂度么?
趁风卷快排的partition函数的空间复杂度是O(1),但整个排序过程是递归的,最多会有O(logn)个函数放在栈里。这一部分不算空间复杂度么?作者回复: 也算的 不过低阶会被忽略
2018-10-1726
收起评论

