23 | 二叉树基础（上）：什么样的二叉树适合用数组来存储？
王争
该思维导图由 AI 生成，仅供参考
前面我们讲的都是线性表结构，栈、队列等等。今天我们讲一种非线性表结构，树。树这种数据结构比线性表的数据结构要复杂得多，内容也比较多，所以我会分四节来讲解。
我反复强调过，带着问题学习，是最有效的学习方式之一，所以在正式的内容开始之前，我还是给你出一道思考题：二叉树有哪几种存储方式？什么样的二叉树适合用数组来存储？
带着这些问题，我们就来学习今天的内容，树！
树（Tree）
我们首先来看，什么是“树”？再完备的定义，都没有图直观。所以我在图中画了几棵“树”。你来看看，这些“树”都有什么特征？
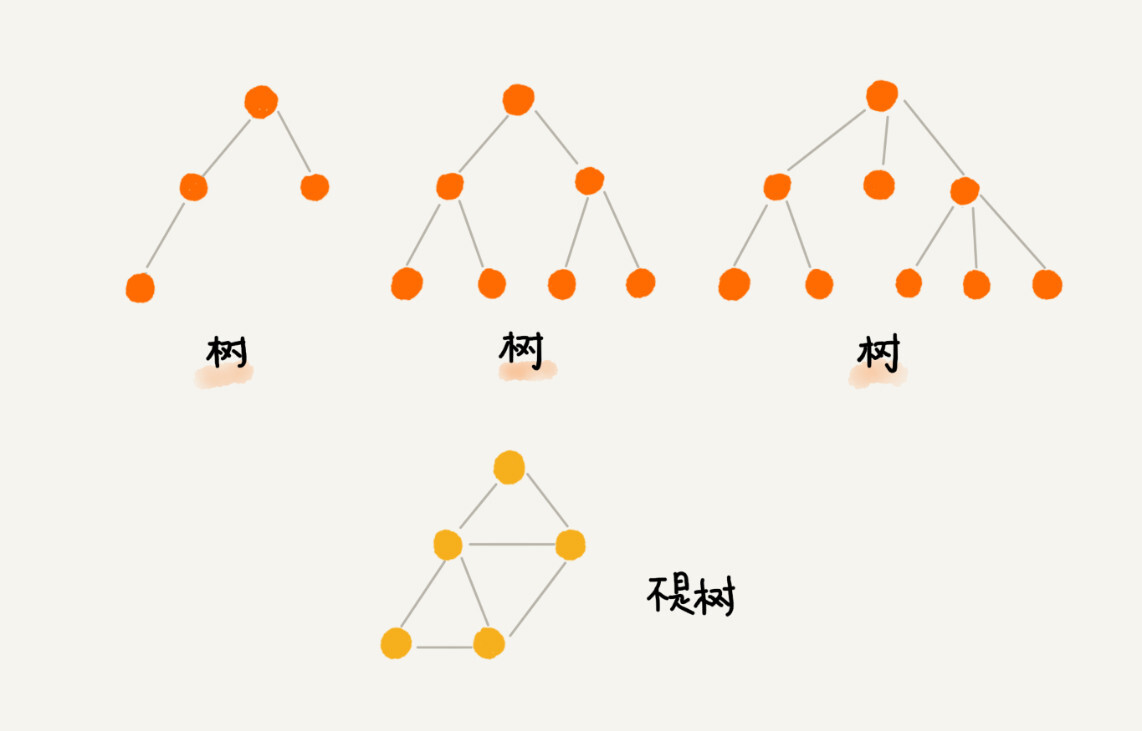
你有没有发现，“树”这种数据结构真的很像我们现实生活中的“树”，这里面每个元素我们叫做“节点”；用来连接相邻节点之间的关系，我们叫做“父子关系”。
比如下面这幅图，A 节点就是 B 节点的父节点，B 节点是 A 节点的子节点。B、C、D 这三个节点的父节点是同一个节点，所以它们之间互称为兄弟节点。我们把没有父节点的节点叫做根节点，也就是图中的节点 E。我们把没有子节点的节点叫做叶子节点或者叶节点，比如图中的 G、H、I、J、K、L 都是叶子节点。
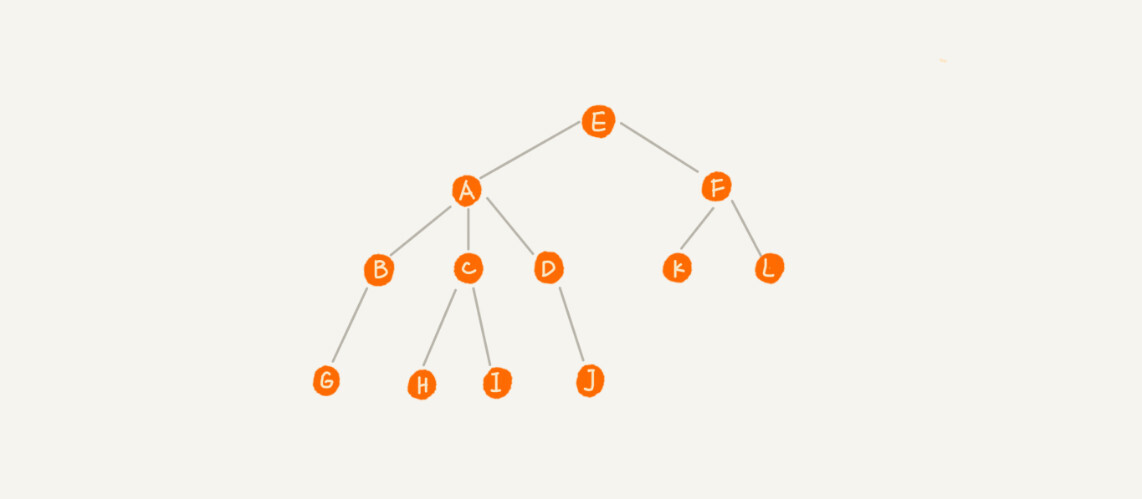
除此之外，关于“树”，还有三个比较相似的概念：高度（Height）、深度（Depth）、层（Level）。它们的定义是这样的：
公开
同步至部落
取消
完成
0/2000
荧光笔
直线
曲线笔记
复制
AI
- 深入了解
- 翻译
- 解释
- 总结
本文深入介绍了二叉树的基础知识和遍历操作。首先，作者详细解释了树的概念，包括节点、父子关系、高度、深度和层等概念。随后，对二叉树进行了深入讨论，包括满二叉树和完全二叉树的特点，以及二叉树的两种存储方式。其中，作者强调了完全二叉树用数组存储是最节省内存的方式。此外，文章还介绍了二叉树的前、中、后序遍历操作，并给出了递归实现的代码。最后，作者指出二叉树遍历的时间复杂度为O(n)。总的来说，本文内容详实，适合初学者了解二叉树的基础知识和遍历操作。文章内容涵盖了树的基本概念、二叉树的特点和存储方式，以及遍历操作的实现和时间复杂度。对于对二叉树感兴趣的读者来说，这篇文章是一份很好的参考资料。
仅可试看部分内容，如需阅读全部内容，请付费购买文章所属专栏
《数据结构与算法之美》，新⼈⾸单¥68
《数据结构与算法之美》，新⼈⾸单¥68
立即购买
© 版权归极客邦科技所有，未经许可不得传播售卖。 页面已增加防盗追踪，如有侵权极客邦将依法追究其法律责任。
登录 后留言
全部留言(254)
- 最新
- 精选
- meng关于问题1，如果是完全二叉树，老师说过可以放在数组里面，那么问题是否 可以简化为数组内的元素有多少种组合方式，这样的话，就是 n!，不知是否可以这样理解 ？
作者回复: 👍
2018-11-1828571 
言志1、既然是数组了，说明是完全二叉树，应该有n的阶乘个组合。 2、二叉树按层遍历，可以看作以根结点为起点，图的广度优先遍历的问题。作者回复: 👍
2018-11-214122
天二老师 你在计算便利二叉树时间复杂度的时候说，“从我前面画的前、中、后序遍历的顺序图，可以看出来，每个节点最多会被访问两次”， 我想知道都是哪两次呢？ 可否帮忙解惑，从图中没看出来作者回复: 第一次遍历到的时候算一次。递归返回的时候再一次。不过，这些说法都很笼统，你只要知道每个节点都被访问了一次，并且被访问的次数是常数次就可以了。
2019-01-2146
Spider Man现在评论的小伙伴少了好多，坚持学习的小伙伴是不是越来越少了？大家的热情呢？💪作者回复: 有些人学得慢 或者工作耽搁了。一直追着最新的看的不多
2018-11-211435- Jamin关于树的高度和深度 目前没有统一的规范，有的是从0开始计算，有的是从1开始
作者回复: 那就按照我的来吧：）我觉得我定义的很有道理：）
2019-01-23319 
星君应该讲讲非递归遍历啊，递归遍历太简单，后序非递归遍历才是难点作者回复: 专栏有自己的定位的 太难没啥用的 不怎么会讲的 自己研究吧
2018-11-28314
talk is cheap！老师，完全二叉树把最底一层去掉，是不是就是一颗满二叉树呢？作者回复: 是的 没错
2019-05-0610
nothing后序遍历节点不是最多被访问三次嘛， 还有那个深度我们学的深度和层次是一样的哇作者回复: 1 从图上看是两次 2 从生活中的理解来说 应该没有第0层之说 但是有深度为0的说法
2018-11-125
D→_→M老师是否可以在您专栏的github上传一下二叉树这几节的相关代码，还有除了递归遍历二叉树，循环遍历是否也可以讲一下，或者在github上上传一下相关代码，自行研究学习。作者回复: 非递归遍历比较复杂 不建议非得给自己制造学习难度 除非是为了面试。其他的二叉树的代码我会放到github上
2018-11-124
传说中的成大大刚刚思考了完全二叉树的定义 叶子结点必须要在最后两层 如果不在最后两层的话通过数组顺序存储也会浪费空间吧作者回复: 是的
2018-11-123
收起评论
