15 | 二分查找(上):如何用最省内存的方式实现快速查找功能?
王争

该思维导图由 AI 生成,仅供参考
今天我们讲一种针对有序数据集合的查找算法:二分查找(Binary Search)算法,也叫折半查找算法。二分查找的思想非常简单,很多非计算机专业的同学很容易就能理解,但是看似越简单的东西往往越难掌握好,想要灵活应用就更加困难。
老规矩,我们还是来看一道思考题。
假设我们有 1000 万个整数数据,每个数据占 8 个字节,如何设计数据结构和算法,快速判断某个整数是否出现在这 1000 万数据中? 我们希望这个功能不要占用太多的内存空间,最多不要超过 100MB,你会怎么做呢?带着这个问题,让我们进入今天的内容吧!
无处不在的二分思想
二分查找是一种非常简单易懂的快速查找算法,生活中到处可见。比如说,我们现在来做一个猜字游戏。我随机写一个 0 到 99 之间的数字,然后你来猜我写的是什么。猜的过程中,你每猜一次,我就会告诉你猜的大了还是小了,直到猜中为止。你来想想,如何快速猜中我写的数字呢?
假设我写的数字是 23,你可以按照下面的步骤来试一试。(如果猜测范围的数字有偶数个,中间数有两个,就选择较小的那个。)
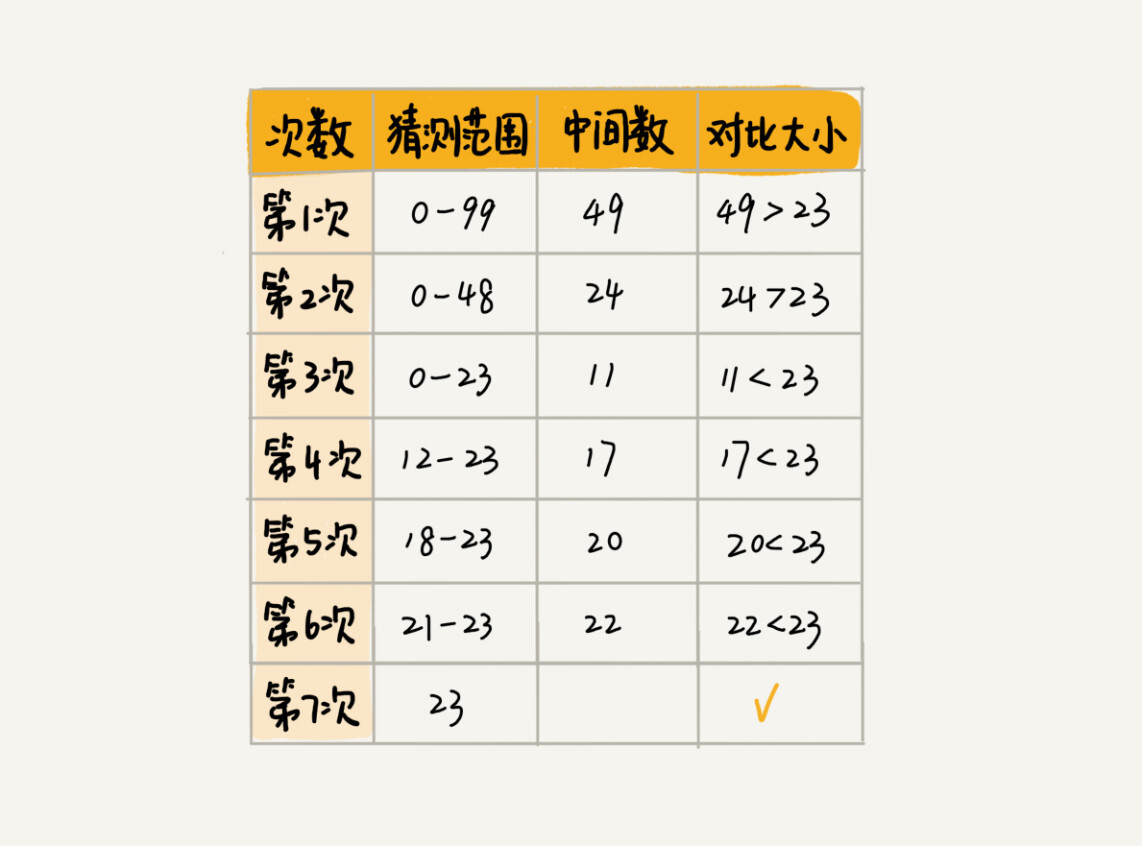
7 次就猜出来了,是不是很快?这个例子用的就是二分思想,按照这个思想,即便我让你猜的是 0 到 999 的数字,最多也只要 10 次就能猜中。不信的话,你可以试一试。
公开
同步至部落
取消
完成
0/2000
笔记
复制
AI
- 深入了解
- 翻译
- 解释
- 总结

二分查找算法是一种高效的针对有序数据集合的查找算法,具有O(logn)的时间复杂度。文章通过生动的例子和清晰的代码实现,深入浅出地介绍了二分查找算法的原理和应用。它强调了二分查找的高效性和对数时间复杂度的优越性,同时指出了其应用场景的局限性。二分查找适用于静态数据集合,对于频繁插入、删除操作的动态数据集合则不再适用。此外,文章还提到了二分查找对数据结构的要求,只能用在有序的顺序表结构上,且数据量太小或太大时也不适合。总的来说,二分查找是一种高效的查找算法,但应用场景有限,需要根据具体情况选择合适的查找算法。
仅可试看部分内容,如需阅读全部内容,请付费购买文章所属专栏
《数据结构与算法之美》,新⼈⾸单¥68
《数据结构与算法之美》,新⼈⾸单¥68
立即购买
© 版权归极客邦科技所有,未经许可不得传播售卖。 页面已增加防盗追踪,如有侵权极客邦将依法追究其法律责任。
登录 后留言
全部留言(254)
- 最新
- 精选
 Jerry银银置顶说说第二题吧,感觉争议比较大: 假设链表长度为n,二分查找每次都要找到中间点(计算中忽略奇偶数差异): 第一次查找中间点,需要移动指针n/2次; 第二次,需要移动指针n/4次; 第三次需要移动指针n/8次; ...... 以此类推,一直到1次为值 总共指针移动次数(查找次数) = n/2 + n/4 + n/8 + ...+ 1,这显然是个等比数列,根据等比数列求和公式:Sum = n - 1. 最后算法时间复杂度是:O(n-1),忽略常数,记为O(n),时间复杂度和顺序查找时间复杂度相同 但是稍微思考下,在二分查找的时候,由于要进行多余的运算,严格来说,会比顺序查找时间慢 ----------------- 以上分析,不知道是否准确,还请老师解答
Jerry银银置顶说说第二题吧,感觉争议比较大: 假设链表长度为n,二分查找每次都要找到中间点(计算中忽略奇偶数差异): 第一次查找中间点,需要移动指针n/2次; 第二次,需要移动指针n/4次; 第三次需要移动指针n/8次; ...... 以此类推,一直到1次为值 总共指针移动次数(查找次数) = n/2 + n/4 + n/8 + ...+ 1,这显然是个等比数列,根据等比数列求和公式:Sum = n - 1. 最后算法时间复杂度是:O(n-1),忽略常数,记为O(n),时间复杂度和顺序查找时间复杂度相同 但是稍微思考下,在二分查找的时候,由于要进行多余的运算,严格来说,会比顺序查找时间慢 ----------------- 以上分析,不知道是否准确,还请老师解答作者回复: 分析的很好 👍 同学们可以把这条顶上去了
2018-10-25331145- 蒋礼锐置顶因为要精确到后六位,可以先用二分查找出整数位,然后再二分查找小数第一位,第二位,到第六位。 整数查找很简单,判断当前数小于+1后大于即可找到, 小数查找举查找小数后第一位来说,从x.0到(x+1).0,查找终止条件与整数一样,当前数小于,加0.1大于, 后面的位数以此类推,可以用x*10^(-i)通项来循环或者递归,终止条件是i>6, 想了一下复杂度,每次二分是logn,包括整数位会查找7次,所以时间复杂度为7logn。空间复杂度没有开辟新的储存空间,空间复杂度为1。 没有具体用代码实现,只是思路,还请多多指正。之后会用js去实际实现。2018-10-2415123
 Jerry银银个人觉得二分查找进行优化时,还个细节注意: 将mid = lo + (hi - lo) /2,将除法优化成移位运算时,得注意运算符的优先级,千万不能写成这样:mid = lo + (hi - lo) >> 1
Jerry银银个人觉得二分查找进行优化时,还个细节注意: 将mid = lo + (hi - lo) /2,将除法优化成移位运算时,得注意运算符的优先级,千万不能写成这样:mid = lo + (hi - lo) >> 1作者回复: 👍
2018-10-2615314 Alexis何春光现在在cmu读研,正在上terry lee的data structure,惊喜的发现不少他讲的点你都涵盖了,个别他没讲到的你也涵盖了.... (当然可能因为那门课只有6学时,时间不足,但还是给这个专栏赞一个!)
Alexis何春光现在在cmu读研,正在上terry lee的data structure,惊喜的发现不少他讲的点你都涵盖了,个别他没讲到的你也涵盖了.... (当然可能因为那门课只有6学时,时间不足,但还是给这个专栏赞一个!)作者回复: 读cmu 太厉害了 仰慕
2018-11-1224213- 刘伟、关于1000万数中快速查找某个整数,我有个想法。考虑用数组下标来存储数据,一个bit位来存储标记。第一次排序的时候能得到这组数的最大值和最小值。 假如最小是5,最大是2000万。那我们定义一个字节数组Byte arr[2000万],因为我只需要打标记,所以一个bit能存下标记,一个byte能存8个数。只需要2MB多一点就能存2000万个数的状态(存在还是不存在) 先把这1000万个数存进去,用数x/8得到下标。用数x%8得到余数,因为每8个数一组得到的数组下标相同,所以还需要通过余数来确定具体是哪一个数。之后开始设置状态,从低位到高位,每一位代表一个数的状态,case0到7,每一次设置当下号码的状态时,先用按位于计算把其他不相关位置为1,当前位置为0,然后按位或对当前位置设置状态。存在就设置位1 ,不存在就设置位0 上述操作执行完之后,就支持任意查找了。只需要输入一个数x,我就能立刻通过x/8和x%8得到当前这个数的位置,然后把这个位置的状态位数字取出来。如果是1表示存在,如果是0表示不存在。 不知道这个想法有没有什么漏洞。希望老师或者一起学习的同学能帮忙一起想想
作者回复: 赞 不错!
2019-06-021341  THROW1000w数据查找这个,在排序的时候不就可以找到了么?
THROW1000w数据查找这个,在排序的时候不就可以找到了么?作者回复: 如果是多次查找操作呢
2018-10-24634 Garwen第一题虽说是在二分查找的这一章,还是推荐大家用牛顿弦切法求解平方根,代码如下供大家参考: double number = 15; //待求平方根的数 double xini = 10;//初始点 while(xini*xini - number > 1e-6) { xini = (number + xini*xini)/2/xini; }
Garwen第一题虽说是在二分查找的这一章,还是推荐大家用牛顿弦切法求解平方根,代码如下供大家参考: double number = 15; //待求平方根的数 double xini = 10;//初始点 while(xini*xini - number > 1e-6) { xini = (number + xini*xini)/2/xini; }作者回复: 👍
2018-11-21422 王小李平方根可以用牛顿迭代实现。
王小李平方根可以用牛顿迭代实现。作者回复: 哈哈 同学的回答超纲了 👍
2018-10-24220- 追风者王老师,考研的话可以以这个课程作为数据结构第一轮的基础复习吗。如果可以,还需要补充其他概念知识吗
作者回复: 概念知识应该全了 考研的话还要看看考纲吧
2018-10-246  王博一个整数占八个字节吗???
王博一个整数占八个字节吗???作者回复: 这个跟计算机硬件、编程语言都有关系的。
2019-02-2324
收起评论

