30 | 无向图模型：马尔可夫随机场
王天一
该思维导图由 AI 生成，仅供参考
作为有向图模型的代表，贝叶斯网络将随机变量之间的条件独立性与依赖关系嵌入到图结构之中，既有助于直观表示，又能简化计算。但这是不是意味着贝叶斯网络可以通吃所有概率关系呢？并非如此。
下面这个例子就说明了贝叶斯网络的局限之处，它取自达芙妮·科勒（Daphne Koller）的经典教材《概率图模型》（Probabilistic Graphical Models）的例 3.8。
“四个学生 Alice、Bob、Charles 和 Debbie 在一个学习小组中，但由于 A 和 C、B 和 D 两两之间因为感情的纠葛导致没有交流，因此每个人可以交流的对象都只有 2 个。这样的关系应该如何表示呢？”
这四个学生可以建模成概率图中的四个结点，也就是四个随机变量。用贝叶斯网络构造这组关系时，由于 A 和 C 之间不存在交流，两者之间也就没有信息的流动，所以在给定 B 和 D 的前提下，A 和 C 是条件独立的；同样的道理，在给定 A 和 C 的前提下，B 和 D 也是条件独立的。这就要求构造出来的贝叶斯网络能够同时表示这两组条件独立性。
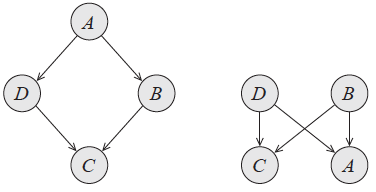
贝叶斯网络的局限性（图片来自 Probabilistic Graphical Models，图 3.10）
上图表示的是两种可能的贝叶斯网络结构，但两者都没法同时表示两个条件独立性。在左侧的子图中，从 A 到 C 的两条通路都是顺连结构，中间的结点分别是 B 和 D。固定的 B 和 D 堵塞了信息流动的通道，从而保证了 A 和 C 的条件独立性。
公开
同步至部落
取消
完成
0/2000
荧光笔
直线
曲线笔记
复制
AI
- 深入了解
- 翻译
- 解释
- 总结
马尔可夫随机场是一种重要的概率图模型，与贝叶斯网络相比，它不具有边的方向性，允许存在环路结构，适用于处理随机变量之间的相互作用和循环依赖关系的建模。马尔可夫随机场的结构通过因子来描述变量之间的相互作用，并且可以通过因子分解等价于吉布斯分布。文章介绍了马尔可夫随机场的条件独立性，包括全局性、局部性和成对性，以及在Python中使用pgmpy建模马尔可夫随机场的方法。此外，文章还探讨了马尔可夫随机场与贝叶斯网络之间的相互转化，以及马尔可夫随机场在图像处理中的广泛应用，如图像分割、去噪、目标识别等计算机视觉任务。总的来说，马尔可夫随机场在概率图模型中具有重要地位，对读者快速了解其基本原理和应用具有重要参考价值。
仅可试看部分内容，如需阅读全部内容，请付费购买文章所属专栏
《机器学习 40 讲》，新⼈⾸单¥59
《机器学习 40 讲》，新⼈⾸单¥59
立即购买
© 版权归极客邦科技所有，未经许可不得传播售卖。 页面已增加防盗追踪，如有侵权极客邦将依法追究其法律责任。
登录 后留言
全部留言(4)
- 最新
- 精选
夏震华(围巾)老师能提个意见不，code 可以加注释吗! 这段代码我看不懂，实在是不知道在做什么。。。 model = MarkovModel([('A', 'B'), ('B', 'C'), ('C', 'D'), ('D', 'A')]) model.add_factors(phi_1, phi_2, phi_3, phi_4) phi = phi_1 * phi_2 * phi_3 * phi_4 Z = model.get_partition_function() normalized = phi.values / Z print(normalized)作者回复: 因为使用的编辑器不支持中文注释，索性就没有添加了。 这段代码的内容是建立马尔可夫网的模型，并定义网络节点之间的依赖关系，比如AB两个变量之间存在关联，它们之间的因子函数被定义为phi_1。整个网络的因子函数就是每个单独因子的乘积。 因子函数不满足归一化的条件，所以要把它改写成概率的形式，就必须进行额外的归一化，后面两行就是归一化的过程。 至于代码中具体函数的用法，可以参考pgmpy的文档，里面也有说明。
2018-11-081
林彦请问老师马尔可夫随机场中的3种形式的条件独立性(马尔可夫性)是同时都成立吗？就是只要是马尔科夫随机场，就满足这种条件独立性？谢谢。作者回复: 三个强度不一样，全局>局部>成对
2018-08-31
Trinity这部分如果有个形象的例子就更好了2021-01-23- 林彦马尔可夫随机场在图像处理中的应用我的理解是根据图像中每个像素点的邻域标签来优化其标签。抽象来看分割，去噪和目标识别都可以用这个方法来处理。 这里可以用一种不够精确的像素分类先保证大多数图像有一个较准确的分类，再应用马尔可夫随机场令图像中某一点的特性或分类只与其附近的邻域有关。图像中的每一个像素就代表概率图模型中的顶点。在随机场中，利用邻域系统可以分析空间上的马尔科夫性：一个像素点的特性，更可能受它周围像素的影响，与它距离越远的像素，对它的特性的影响越小。邻域系统定义了图像中一个像素（中心像素），受周围哪些像素的影响。中心像素和相邻像素一起，构成的集合就是团(clique)。 具体计算中用吉布斯分布的密度函数来计算标记(标签)场的先验概率，即求周围像素点中各个标签出现的概率多大，然后用高斯分布的密度函数求解所求像素点属于哪个标签的概率最大，即这个像素点的条件概率（似然函数）。根据贝叶斯公式目标就是寻找这2个函数值乘积最大的分类标签。2018-08-31
收起评论