机器学习40讲
王天一
工学博士，副教授
立即订阅
8040 人已学习
课程目录
已完结 44 讲
0/4登录后，你可以任选4讲全文学习。
开篇词 (1讲)
开篇词 | 打通修炼机器学习的任督二脉
免费
机器学习概观 (10讲)
01 | 频率视角下的机器学习
02 | 贝叶斯视角下的机器学习
03 | 学什么与怎么学
04 | 计算学习理论
05 | 模型的分类方式
06 | 模型的设计准则
07 | 模型的验证方法
08 | 模型的评估指标
09 | 实验设计
10 | 特征预处理
统计机器学习模型 (18讲)
11 | 基础线性回归：一元与多元
12 | 正则化处理：收缩方法与边际化
13 | 线性降维：主成分的使用
14 | 非线性降维：流形学习
15 | 从回归到分类：联系函数与降维
16 | 建模非正态分布：广义线性模型
17 | 几何角度看分类：支持向量机
18 | 从全局到局部：核技巧
19 | 非参数化的局部模型：K近邻
20 | 基于距离的学习：聚类与度量学习
21 | 基函数扩展：属性的非线性化
22 | 自适应的基函数：神经网络
23 | 层次化的神经网络：深度学习
24 | 深度编解码：表示学习
25 | 基于特征的区域划分：树模型
26 | 集成化处理：Boosting与Bagging
27 | 万能模型：梯度提升与随机森林
总结课 | 机器学习的模型体系
概率图模型 (14讲)
28 | 最简单的概率图：朴素贝叶斯
29 | 有向图模型：贝叶斯网络
30 | 无向图模型：马尔可夫随机场
31 | 建模连续分布：高斯网络
32 | 从有限到无限：高斯过程
33 | 序列化建模：隐马尔可夫模型
34 | 连续序列化模型：线性动态系统
35 | 精确推断：变量消除及其拓展
36 | 确定近似推断：变分贝叶斯
37 | 随机近似推断：MCMC
38 | 完备数据下的参数学习：有向图与无向图
39 | 隐变量下的参数学习：EM方法与混合模型
40 | 结构学习：基于约束与基于评分
总结课 | 贝叶斯学习的模型体系
结束语 (1讲)
结课 | 终有一天，你将为今天的付出骄傲
机器学习40讲
登录|注册
26 | 集成化处理：Boosting与Bagging
王天一 2018-08-02
伊壁鸠鲁（Epicurus）是古希腊一位伟大的哲学家，其哲学思想自成一派。在认识论上，伊壁鸠鲁最核心的观点就是“多重解释原则”（Prinicple of Multiple Explanantions），其内容是当多种理论都能符合观察到的现象时，就要将它们全部保留。这在某种程度上可以看成是机器学习中集成方法的哲学基础。
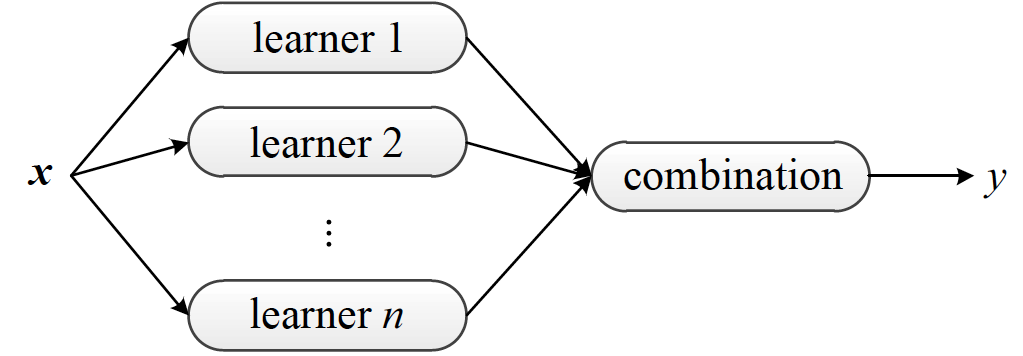
集成学习架构图（图片来自 Ensemble Methods: Foundations and Algorithms，图 1.9）
集成学习的常用架构如上图所示。在统计学习中，集成学习（ensemble learning）是将多个基学习器（base learners）进行集成，以得到比每个单独基学习器更优预测性能的方法。每个用于集成的基学习器都是弱学习器（weak learner），其性能可以只比随机猜测稍微好一点点。
集成学习的作用就是将这多个弱学习器提升成一个强学习器（strong learner），达到任意小的错误率。
在设计算法之前，集成学习先要解决的一个理论问题是集成方法到底有没有提升的效果。虽说三个臭皮匠赛过诸葛亮，但如果皮匠之间没法产生化学反应，别说诸葛亮了，连个蒋琬、费祎恐怕都凑不出来。
在计算学习的理论中，这个问题可以解释成弱可学习问题（weakly learnable）和强可学习问题（strongly learnable）的复杂性是否等价。幸运的是，这个问题的答案是“是”，而实现从弱到强的手段就是提升方法。
取消
完成
0/1000字
划线
笔记
复制
© 版权归极客邦科技所有，未经许可不得传播售卖。 页面已增加防盗追踪，如有侵权极客邦将依法追究其法律责任。
该试读文章来自付费专栏《机器学习40讲》，如需阅读全部文章，
请订阅文章所属专栏。
请订阅文章所属专栏。
立即订阅
登录 后留言
精选留言(4)
我心飞扬MultiBoosting由于集合了Bagging，Wagging，AdaBoost，可以有效的降低误差和方差，特别是误差。但是训练成本和预测成本都会显著增加。
Iterative Bagging相比Bagging会降低误差，但是方差上升。由于Bagging本身就是一种降低方差的算法，所以Iterative Bagging相当于Bagging与单分类器的折中。作者回复: 总结得很到位👍
2018-08-02 1- InsomniaTony如果对基于决策树的方法感兴趣的话，可以看Gilles Louppe的博士毕业论文Understanding Random Forest。个人觉得很有帮助
作者回复: 感谢推荐！
2018-10-20 
林彦MultiBoosting如果不引入有泊松分布的权重来对样本作wagging，不知道在性能和效果上是否能比Adaboost达到更好的平衡。
Iterative Boosting方法的文章不好找，有没有更具体的称呼。
从实践中看，这几年GBDT，XGBoost，Random Forest太好用了。除了它们和基本的几类集成学习方法外，介绍其他的延伸集成学习方法通俗易懂，正确，且不只是概述的中文文章在学术领域之外很少。作者回复: Multiboosting相当于AdaBoost和wagging的结合，wagging的作用主要在于通过随机的样本权重扰动降低方差。去掉wagging也就是普通的AdaBoost了。
你说的是iterative bagging吗？可以参考2001年Leo Breiman的论文Using iterated bagging to debias regressions。这种方法也叫adaptive bagging，诞生快20年一直不温不火，没受到多少关注。2018-08-18
周平没看太懂，需要多次学习2018-08-03
收起评论