14 | 非线性降维：流形学习
该思维导图由 AI 生成，仅供参考
荧光笔
直线
曲线- 深入了解
- 翻译
- 解释
- 总结
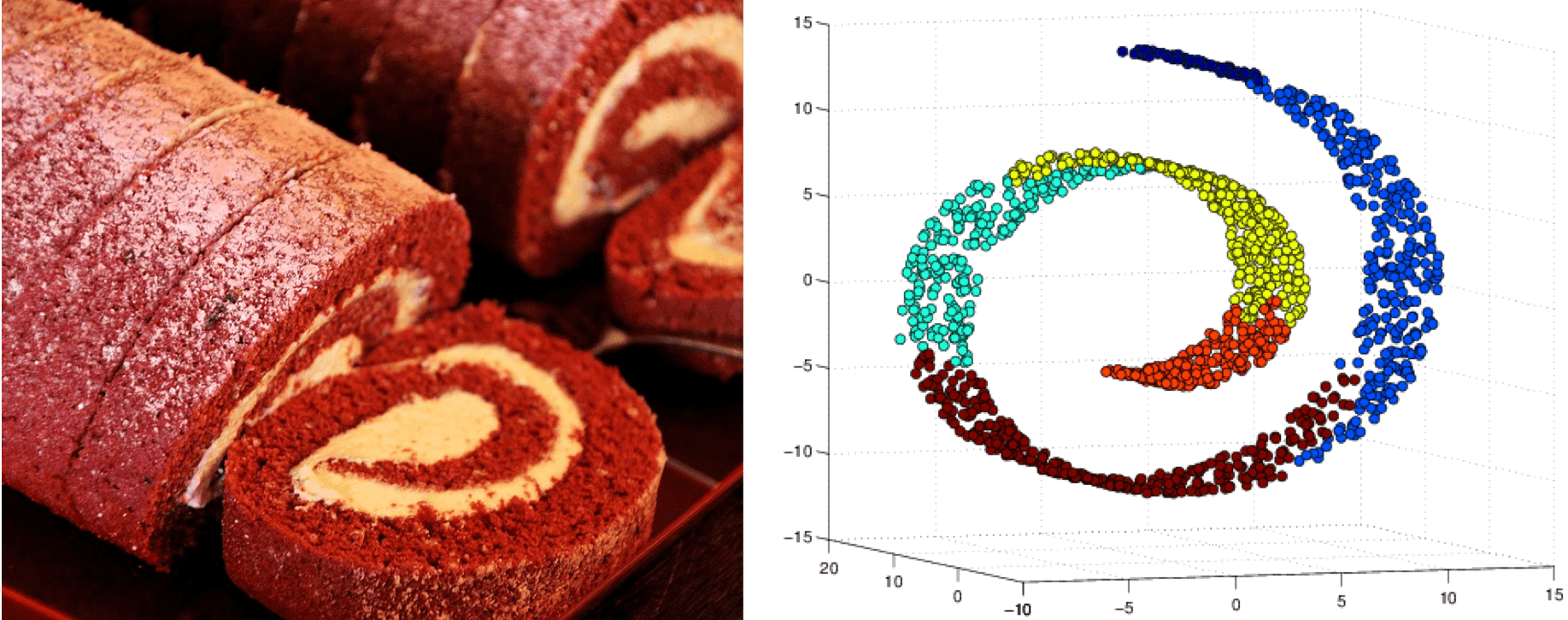
流形学习是一种非线性降维方法，旨在发现高维数据的低维嵌入流形。该方法包括等度量映射、局部线性嵌入和$t$分布随机近邻嵌入等典型算法。等度量映射基于全局信息，通过测地距离和欧氏距离的等效性计算流形；而局部线性嵌入则基于局部信息，通过局部线性系数的不变性计算流形。$t$分布随机近邻嵌入将欧氏距离映射为相似性，利用相似性的保持计算流形。这些方法的应用可以将复杂的高维数据映射到二维或三维流形上，从而实现数据的可视化和隐藏结构的挖掘。流形学习与主成分分析相比，能够揭示数据的结构，而主成分分析则更适用于揭示数据的规律。因此，流形学习在数据可视化和特征识别方面具有重要作用。在实际应用中，Scikit-learn中的manifold模块提供了常用的流形学习方法，使得算法的细节被隐藏在函数内部，用户只需输入对应的参数即可。总之，流形学习是一种重要的非线性降维方法，对于理解数据的结构和特征识别具有重要意义。
《机器学习 40 讲》，新⼈⾸单¥59
全部留言(9)
- 最新
- 精选
林彦如文中所述，降维和对于数据结构更好的解读是流形学习的应用。具体应用上在图像领域，特别是一些我们人脑能理解的图像信息的变化，比如苹果的各种品种，图像中一个物体的角度或位置的变化，流形学习理论上比线性降维能更好地关联数据的“关键”特征。 网上搜索结果中，流形学习在人脸识别的应用比较多。Bengio的《Deep Learning》中提到“在图像中，我们当然会认为有很多可能的变换仍然允许我们描绘出图片空间的流形:我们可以逐渐变暗或变亮光泽、逐步移动或旋转图中对象、逐渐改变对象表面的颜色等等。在大多数应用中很有可能会涉及到多个流形“。其中提到的2个人脸的例子里展示了人脸图像的高维流形到低维的映射，这些低维可以对应不同轴向的旋转，人的情绪表达。别的例子里提到了光照。 《Deep Learning》中的第2个例子提到了流形和自编码器的关系，我的理解是和多种自编码器的理论解读都有关系，如去噪自编码器，收缩自编码器，变分自编码器。生成式对抗网络的一些文章描述里也提及了流形，但我不确认和流形学习中的流形是否相关。 无监督学习或半监督学习发现或推导未知的数据特征时，流形学习有应用的场景(未读相关论文，有可能更偏向理论)。作者回复: 自编码器里的隐藏层神经元会少于输入的数目，从降维的角度来说，可以归到流形的范畴。但真正比较实在的应用是在知乎上看到的在生物行为学中的使用，一篇典型的论文是Mapping the stereotyped behavior of freely moving fruit flies。
2018-07-062
paradox老师，您好 文中t分布随机近邻嵌入改进的一方面是，让低维空间中的条件分布服从t分布，是不是因为t分布的自由度可以加入限制条件？不是很理解它的作用作者回复: 你可以观察下高斯分布和t分布的形状比较，t分布的长尾特性让它对距离的保持性更好。高维空间上相距较远的点被压缩到低维空间之后可能会变得很近，但它们之间并没有什么相似性，这就是文中提到的拥挤问题。t分布能够把高维空间上距离较远的点映射成低维空间上同样距离较远的点，从而把同一类点聚合，把不同类的点分开。
2018-08-10
VentusDeus老师，感觉这一季的内容很有意思 在上一季基础上又有更多对数学原理更为深入和一般化的的讨论。不知道还会不会考虑像上一季一样推出一些参考书目/论文供大家深入学习了呢？作者回复: 有的，在总结部分会系统地推荐一些书目。
2018-07-07
zhoujie流形学习是非参数的，因此对噪声会计较敏感，那有没有办法让流形学习不那么敏感呢？作者回复: 这是非常好的研究方向。
2018-07-06
Python要是能结合到生活中讲就好了，这样写的太抽象了2018-12-2513- 赵晓叶有案例对应的完整代码吗2023-08-22归属地：上海
ifelse
学习打卡2023-06-01归属地：浙江
建强个人比较肤浅的理解是，流形学习通过把样本数据从高纬空间投影到低纬空间来揭示样本之间的内在关系，变化的趋势等，这样只要把样本投影到由样本特征组成的不同低维空间中，就能从不同的侧面来反映样本的关系和变化规律，而主成份分析只是在数据的主要特征上反映数据的变化规律和关系，不能全面揭示样本潜在的内部联系。2021-03-08
极客时间攻城狮学习了2018-08-22