18 人工神经网络 | 左手信号，右手误差：多层感知器
王天一
该思维导图由 AI 生成，仅供参考
虽然异或问题成为感知器和早期神经网络的阿喀琉斯之踵，但它并非无解的问题。恰恰相反，解决它的思路相当简单，就是将单层感知器变成多层感知器。下图就是一个多层感知器的实例，这个包含单个隐藏层的神经网络能够完美地解决异或问题。
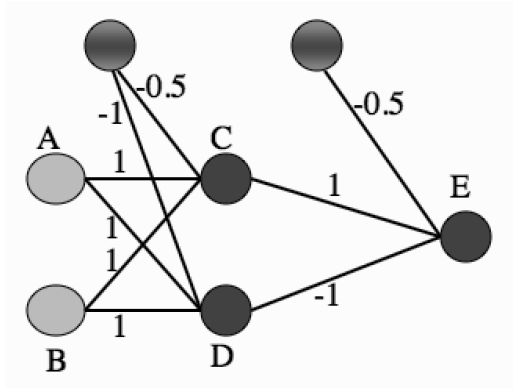
（图片来自Machine Learning: An Algorithmic Perspective, 2nd Edition, Figure 4.2）
假定两个输入节点 A 和 B 的二进制输入分别为 1 和 0，则根据图中的权重系数可以计算出神经元 C 的输入为 0.5，而神经元 D 的输入为 0。在由 C 和 D 构成的隐藏层中，由于 C 的输入大于 0，因而符号函数使其输出为 1；由于 D 的输入等于 0，符号函数则使其输出为 0。在输出节点的神经元 E 上，各路输入线性组合的结果为 0.5，因而 E 的输出，也是神经网络整体的输出，为 1，与两个输入的异或相等。在此基础上可以进一步证明，这个神经网络的运算规则就是异或操作的运算规则。
多层感知器（multilayer perceptron）包含一个或多个在输入节点和输出节点之间的隐藏层（hidden layer），除了输入节点外，每个节点都是使用非线性激活函数的神经元。而在不同层之间，多层感知器具有全连接性，即任意层中的每个神经元都与它前一层中的所有神经元或者节点相连接，连接的强度由网络中的权重系数决定。多层感知器是一类前馈人工神经网络（feedforward neural network）。网络中每一层神经元的输出都指向输出方向，也就是向前馈送到下一层，直到获得整个网络的输出为止。
多层感知器的训练包括以下步骤：首先确定给定输入和当前权重下的输出，再将输出和真实值相减得到误差函数，最后根据误差函数更新权重。在训练过程中，虽然信号的流向是输出方向，但计算出的误差函数和信号传播的方向相反，也就是向输入方向传播的，正因如此，这种学习方式得名反向传播（backpropagation）。反向传播算法通过求解误差函数关于每个权重系数的偏导数，以此使误差最小化来训练整个网络。
在反向传播算法中，首先要明确误差函数的形式。当多层感知器具有多个输出时，每个分类结果 与真实结果 之间都会存在误差。在单层感知器中，误差直接被定义为两者之间的差值。但在多个输出的情形下，如果第一个输出神经元的误差大于零，第二个输出神经元的误差小于零，这两部分误差就可能部分甚至完全抵消，造成分类结果准确无误的假象。
如何避免这个问题呢？
公开
同步至部落
取消
完成
0/2000
荧光笔
直线
曲线笔记
复制
AI
- 深入了解
- 翻译
- 解释
- 总结
多层感知器和反向传播算法是人工神经网络中的重要组成部分。多层感知器通过隐藏层的特征检测和反向传播算法的训练，实现了对复杂问题的解决。文章详细介绍了多层感知器的结构和训练过程，包括隐藏层的作用、误差函数的形式、传递函数的选择以及反向传播算法的流程。此外，文章还提到了多层感知器设计中需要考虑的工程因素，如权重系数的确定和训练数据量的影响。在数学上可以证明，只要隐藏神经元的数目足够多，一个隐藏层就能使多层感知器以任意精度逼近任意复杂度的连续函数。然而，多层感知器的训练也面临着迭代次数、过拟合等问题，需要通过验证集监督和早停等策略来解决。总的来说，多层感知器和反向传播算法为解决复杂问题提供了重要的工具和方法。 文章还提到了反向传播算法的提出者乔弗雷·辛顿的观点，即没有目标函数就无法进行反向传播，因此要实现无监督学习就必须告别反向传播算法。这一观点引发了对于无监督学习和反向传播算法的讨论。文章鼓励读者发表自己的观点，以促进对于这一话题的深入探讨。 总的来说，本文通过介绍多层感知器和反向传播算法的基本原理，以及对于反向传播算法提出者的观点，为读者提供了对于人工神经网络中重要概念的深入理解和思考。
仅可试看部分内容，如需阅读全部内容，请付费购买文章所属专栏
《人工智能基础课》，新⼈⾸单¥59
《人工智能基础课》，新⼈⾸单¥59
立即购买
© 版权归极客邦科技所有，未经许可不得传播售卖。 页面已增加防盗追踪，如有侵权极客邦将依法追究其法律责任。
登录 后留言
全部留言(7)
- 最新
- 精选
JustDoDThttps://google-developers.appspot.com/machine-learning/crash-course/backprop-scroll/ 谷歌的一个反向传播演示页面，很有意思 。作者回复: 谢谢分享！但恐怕要用vpn才能看
2019-09-1723
思考问题的熊一个学习的感受，如果没有相关基础多说内容看一遍是没有什么感觉的。必须看完之后再去翻相关的资料和解释，然后再回过头来看文章，才会有有所感悟。2018-02-1810
陈吉米要是配上点图就更会明白了2018-02-0814- Geek_de85cb这个图解释的不好，只是拿过来这张图，并没有解释上边两个点的含义，对于其中的-0.5，-1，含义都没有解释，也没举例说明：（0，0）（1，0）（0，1）（1，1）四种情况得到的结果为什么是异或的效果，对于新人理解困难较大。2021-08-223
！null开始的图的，不太清楚各个节点的运算法则。第一句：“ C 的输入为 0.5，而神经元 D 的输入为 0”这个结论是咋出来的都不太清楚。2021-09-081- 杨家荣极客时间 21天打卡行动 16/21 <<人工智能基础课18>>多层感知器 回答老师问题: 反向传播算法是在 1986 年由乔弗雷·辛顿提出的，可今天，作为反向传播之父的辛顿却要大义灭亲。辛顿的观点是没有目标函数就无法进行反向传播，而如果数据没有标签自然就没有目标函数了。因此，要实现无监督学习就必须告别反向传播算法。那么应该如何看待辛顿的观点呢？ 前面老师也讲了,无监督算法:聚类(1,k-均值聚类,2,层次聚类,3,基于密度聚类,4高斯混合模型,5,);降维;这类正与监督学习的目标相反,我觉得是对的; 今日所学: 1,多层感知器（multilayer perceptron）包含一个或多个在输入节点和输出节点之间的隐藏层（hidden layer），除了输入节点外，每个节点都是使用非线性激活函数的神经元; 2,多层感知器是一类前馈人工神经网络; 3,多层感知器的训练包括以下步骤：首先确定给定输入和当前权重下的输出，再将输出和真实值相减得到误差函数，最后根据误差函数更新权重。在训练过程中，虽然信号的流向是输出方向，但计算出的误差函数和信号传播的方向相反，也就是向输入方向传播的，正因如此，这种学习方式得名反向传播（backpropagation）。 4,反向传播算法通过求解误差函数关于每个权重系数的偏导数，以此使误差最小化来训练整个网络 5,在反向传播算法中，首先要明确误差函数的形式; 6,在反向传播算法中，每个输出神经元的误差都被写成平方项的形式，整个神经网络的误差则是所有输出神经元的误差之和; 7,明确定义了误差函数后，就要想方设法让它取得最小值。影响误差函数的因素无外乎三个：输入信号、传递函数和权重系数; 8,多层感知器采用对数几率函数作为传递函数; 9,求解误差函数的最小值就要找到误差函数的梯度，再根据梯度调整权重系数，使误差函数最小化; 10,链式法则是个非常有用的数学工具，它的思想是求解从权重系数到误差函数这个链条上每一环的作用，再将每一环的作用相乘，得到的就是链条整体的效果; 11,多层感知器的核心结构就是隐藏层，之所以被称为隐藏层是因为这些神经元并不属于网络的输入或输出。 12,在多层神经网络中，隐藏神经元的作用在于特征检测。随着学习过程的不断进行，隐藏神经元将训练数据变换到新的特征空间之上，并逐渐识别出训练数据的突出特征。 13,一个经验法则是训练样本数目应该是权重系数数目的 10 倍，这显然对计算能力提出了较高的要求; 14,多层感知器的训练要需要多次遍历整个数据集，因而迭代次数就成为另一个重要的问题。预先设定迭代次数无法保证训练效果，预先设定误差阈值则可能导致算法无法终止。因而常用的办法是：一旦误差函数停止减小，就终止学习算法。 15,多层感知器的训练要需要多次遍历整个数据集，因而迭代次数就成为另一个重要的问题。预先设定迭代次数无法保证训练效果，预先设定误差阈值则可能导致算法无法终止。因而常用的办法是：一旦误差函数停止减小，就终止学习算法。 总结: 讲课重点: 1,在感知器的输入层和输出层之间添加隐藏层，就可以得到多层感知器； 2,多层感知器是一类前馈神经网络，采用的是反向传播的学习方式； 3,反向传播算法要根据误差函数的梯度来调整权重系数，需要应用求导的链式法则； 4,单个隐藏层就能使多层感知器以任意精度逼近任意复杂度的连续函数。2020-01-031
- JustDoDT链式法则： https://zh.wikipedia.org/wiki/%E9%93%BE%E5%BC%8F%E6%B3%95%E5%88%992019-09-17
收起评论