15 | 如何用极坐标系绘制有趣图案？

月影



该思维导图由 AI 生成，仅供参考

你好，我是月影。
在前面的课程中，我们一直是使用直角坐标系来绘图的。但在图形学中，除了直角坐标系之外，还有一种比较常用的坐标系就是极坐标系。
极坐标示意图
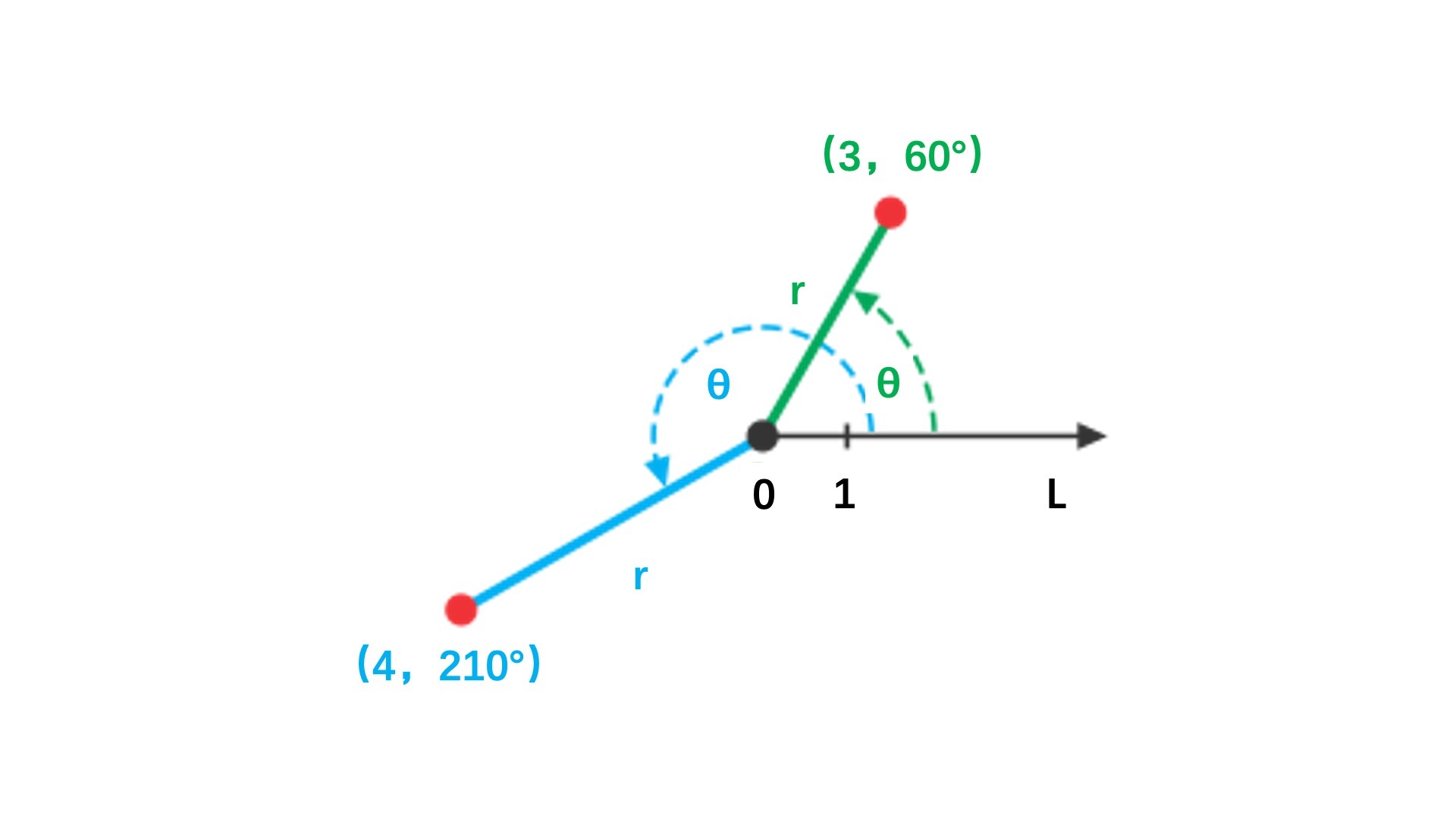
你对极坐标系应该也不陌生，它是一个二维坐标系。与二维直角坐标系使用 x、y 分量表示坐标不同，极坐标系使用相对极点的距离，以及与 x 轴正向的夹角来表示点的坐标，如（3，60°）。
在图形学中，极坐标的应用比较广泛，它不仅可以简化一些曲线方程，甚至有些曲线只能用极坐标来表示。不过，虽然用极坐标可以简化许多曲线方程，但最终渲染的时候，我们还是需要转换成图形系统默认支持的直角坐标才可以进行绘制。在这种情况下，我们就必须要知道直角坐标和极坐标是怎么相互转换的。两个坐标系具体转换比较简单，我们可以用两个简单的函数，toPolar 和 fromPolar 来实现，函数代码如下：
// 直角坐标影射为极坐标
function toPolar(x, y) {
  const r = Math.hypot(x, y);
  const θ= Math.atan2(y, x);
  return [r, θ];
}
// 极坐标映射为直角坐标
function fromPolar(r, θ) {
  const x = r * cos(θ);
  const y = r * sin(θ);
  return [x, y];
}
那今天，我们就通过参数方程结合极坐标，来绘制一些不太好用直角坐标系绘制的曲线，让你认识极坐标的优点，从而帮助你掌握极坐标的用法。
如何用极坐标方程绘制曲线在第 6 节课中，为了更方便地绘制曲线，我们用 parametric.js 函数实现了一个参数方程的绘图模块，它非常方便。所以在使用极坐标方程绘制曲线的时候，我们也要用到 parametric.js 函数。不过，在使用之前，我们还要对它进行扩展，让它支持坐标映射。这样，我们就可以写出对应的坐标映射函数，从而将极坐标映射为绘图需要的直角坐标了。

公开

同步至部落

取消

完成

0/2000

荧光笔

直线

曲线

笔记

复制

AI

深入了解
翻译
英语
中文简体
中文繁体
法语
德语
日语
韩语
俄语
西班牙语
阿拉伯语
解释
总结

本文介绍了极坐标系在绘制有趣图案和角向渐变方面的广泛应用。通过极坐标系和参数方程的结合，读者可以学习如何绘制玫瑰线、心形线、双纽线等有趣的图案，并且了解如何利用片元着色器实现角向渐变效果。文章还展示了如何利用uniform变量来调整图案的形状和颜色，从而创造出更多有趣的视觉效果。此外，读者还可以了解到极坐标系与圆柱坐标系以及球坐标系之间的关系，以及它们在三维图形绘制中的应用。总的来说，本文为读者提供了极坐标系的绘制方法和角向渐变的实现原理，为他们在图形绘制和渐变效果方面提供了新的思路和技术支持。

仅可试看部分内容，如需阅读全部内容，请付费购买文章所属专栏
《跟月影学可视化》，新⼈⾸单¥68

立即购买

登录后留言

全部留言(4)

最新
精选

kylin
老师，能不能介绍一些函数式编程思想的资料，非常想深入学习
作者回复: 这个会在加餐讲的
2020-08-16

2
番薯
第三题被卡住了，请问怎么让fract的每一格随机数不同呢？
2021-02-25
1
1
有一种踏实
随机数映射到 sd 函数的方式，除了用 if 条件语句外，还有其它更优雅的方式吗？ void main() { vec2 st = vUv * 10.0; vec2 p = fract(st); p = p - vec2(0.5); float i = random(floor(st)); float d = 0.0; if (i < 0.33) { d = sdCircle(p, vec2(0.0, 0.0), 0.25); } else if (i >= 0.33 && i < 0.66) { d = sdBox(p, vec2(0.0, 0.0), vec2(0.25)); } else { d = sdApple(p); } gl_FragColor.rgb = mix(vec3(1.0, 0.0, 0.0), vec3(1.0, 1.0, 1.0), smoothstep(0.0, 0.01, d)); gl_FragColor.a = 1.0; }
2023-12-11归属地：上海


有一种踏实
小试牛刀第一题中，为什么旋转极坐标得到的图形变形了？ const fragment = ` #ifdef GL_ES precision highp float; #endif varying vec2 vUv; uniform float u_k; uniform float u_scale; uniform float u_offset; vec2 polar(vec2 st) { return vec2(length(st), atan(st.y, st.x)); } float PI = 3.141592653; void main() { vec2 st = vUv - vec2(0.5); // float rotateRad = PI / 2.0; // mat2 rotateMatrix = mat2( // cos(rotateRad), sin(rotateRad), // -sin(rotateRad), cos(rotateRad) // ); // st = rotateMatrix * st; st = polar(st); st.y = st.y + PI / 2.0; // 这里旋转极坐标得到的图形变形了？ float d = u_scale * 0.5 * abs(cos(st.y * u_k * 0.5)) - st.x + u_offset; gl_FragColor.rgb = smoothstep(-0.01, 0.01, d) * vec3(1.0); gl_FragColor.a = 1.0; } `;
2023-12-11归属地：上海
2


收起评论