08 | 如何利用三角剖分和向量操作描述并处理多边形?

该思维导图由 AI 生成,仅供参考
图形学中的多边形是什么?
- 深入了解
- 翻译
- 解释
- 总结

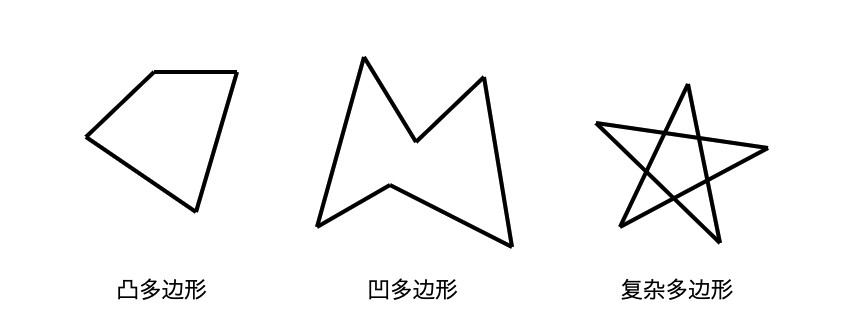
本文深入介绍了图形学中描述和处理多边形的方法,重点讨论了多边形的填充和边界判定。首先解释了多边形的定义和分类,包括简单多边形和复杂多边形,以及凸多边形和凹多边形的区分。详细介绍了在不同的图形系统中采用不同方法来填充多边形,特别是针对WebGL,介绍了利用三角剖分来快速填充多边形的方法。讨论了如何判断点在多边形内部的问题,以及不同图形系统中的判定方法。最后,提出了实现通用的isPointInPath方法,通过点与几何图形的数学关系来判断点是否在图形内部,并给出了相应的代码示例。整体而言,本文通过技术性的讲解和实例演示,帮助读者快速了解了多边形描述和处理的数学方法,以及不同图形系统中的多边形填充技术。文章内容涵盖了图形学中的基本操作和实际应用,对于对图形学感兴趣的读者具有一定的参考价值。文章内容涵盖了图形学中的基本操作和实际应用,对于对图形学感兴趣的读者具有一定的参考价值。
《跟月影学可视化》,新⼈⾸单¥68
全部留言(18)
- 最新
- 精选
- gltjk在之前代码的基础上封装了 Canvas 类和自己的 Vector2D 类,同时增加简单的 WebGL 类(其中封装了用 Tesser2 三角剖分实现的画多边形方法),然后试了试小试牛刀里要求的椭圆、正五角星和菱形星星。因为文件比较多,不用 Codepen 了,改用 Github 放代码。 之后有时间再把判断点在多边形内部做出来,同时把之前 Codepen 的例子迁移过来。 话说感觉 WebGL 好深奥啊,可能我连门都没算入吧…… 在线预览:https://g.gltjk.com/learn-visualization/canvas-webgl-polygon/ 代码仓库:https://github.com/gltjk/learn-visualization
作者回复: 赞👍能动手自己做非常棒,多实践可以快速学习成长。webgl上手不太容易,不过掌握了学习诀窍,打好基础,后面就越来越容易了,而且会觉得越来越有趣
2020-07-09210  Presbyter🎱老师,没脸的问一句。自己已经要疯了,很多数学概念已经不明白了。现在在恶补线性代数,然后在回来看文章。老师能麻烦一下,给出咱们这个课程所需要的数学知识嘛?我好一次性都看了,然后一点一点的在重新读咱们文章。麻烦老师了。
Presbyter🎱老师,没脸的问一句。自己已经要疯了,很多数学概念已经不明白了。现在在恶补线性代数,然后在回来看文章。老师能麻烦一下,给出咱们这个课程所需要的数学知识嘛?我好一次性都看了,然后一点一点的在重新读咱们文章。麻烦老师了。作者回复: 在第9讲的最后我放了一张图,列出了所有的知识点,你可以看一下
2020-07-143 孙华月影大佬 WebGL fill 的例子中 修改一下 gl.drawElements 的渲染模式,将 gl.TRIANGLES 改成 gl.LINE_STRIP。这样,我们就可以清晰地看出,经过 Earcut 处理的这个多边形被分割成了 8 个三角形。 但例子展示的结果中只有6个三角形和一个四边形。这是什么原因?
孙华月影大佬 WebGL fill 的例子中 修改一下 gl.drawElements 的渲染模式,将 gl.TRIANGLES 改成 gl.LINE_STRIP。这样,我们就可以清晰地看出,经过 Earcut 处理的这个多边形被分割成了 8 个三角形。 但例子展示的结果中只有6个三角形和一个四边形。这是什么原因?作者回复: 因为LINE_STRIP是绘制连续线段,所以最终每个点只经过一次,就会出现四边形。不过这里只是大概地显示出三角形形状,所以没关系。如果要严格显示出各个三角形,需要改一下数据,把每个顶点和它的三角形的其他顶点对应的边数据重新存一下然后用LINES绘制
2020-07-242 聂士伟具体实现的算法还需要先判断点是否在多边形外接框矩形内,可以加速
聂士伟具体实现的算法还需要先判断点是否在多边形外接框矩形内,可以加速作者回复: 是的,可以优化
2021-09-191- Geek_b52974简单根据老师给的延伸连结解释一下三角剖分 1. 任相邻的两个三角形一定是组成一个四边形,不会是五边形,六边形 2. 任一三角形的外包圆不可包含其他三角形的顶点 3. 跟 Voronoi diagram 是一体两面的概念,三角剖分中的三角形的边的中垂线相连会成为 Voronoi diagram 中的每个多边型,三角剖分中的顶点称为 Voronoi generators
作者回复: ������
2020-10-1721  嘻嘻话说浏览器的api判断是否在路径内应该也是用的数学方法吧(`・ω・´)ゞ
嘻嘻话说浏览器的api判断是否在路径内应该也是用的数学方法吧(`・ω・´)ゞ作者回复: 具体实现方式要研究浏览器底层实现的源码。我觉得应该是的
2020-10-111- Mingzhang关于判断一个点是否在三角形内(包括边上)我曾经用代数方法做过:对每一条边而言其对应的顶点必然与要判定的点在同一侧,因此需要进行三组测试。判定函数如下: /** * Determine whether p3 and p4 are on the same side of the segment of p1-p2 * @param p1 * @param p2 * @param p3 * @param p4 * returns -1 (not on the same side) | 0 (at least one is on the segment) | 1 (on the same side) */ function onSameSide(p1=[0,0], p2=[0,0], p3=[0,0], p4=[0,0]) { let angle0 = Math.atan2(p2[1] - p1[1], p2[0] - p1[0]); let angle1 = Math.atan2(p3[1] - p1[1], p3[0] - p1[0]); let angle2 = Math.atan2(p4[1] - p1[1], p4[0] - p1[0]); let product = (angle1 - angle0) * (angle2 - angle0); if (product === 0) { return 0; } return product > 0 ? 1 : -1; }
作者回复: 嗯,算atan很消耗性能
2020-07-2721 - 王钰老师,判断 u1 是否在 a 上,是否可以用 |a - u1| > 0 判断,大于 0 时,u1 不在 a 上,等于 0 时在 a 上。
作者回复: 不可以的,除非a和u1的长度相同
2021-07-22  谭鹏github上的代码 怎么打开都是大白屏
谭鹏github上的代码 怎么打开都是大白屏作者回复: 因为qhres域名有问题,换成qhres2就可以了
2021-07-05
 kylin月影老师,您好,请问三角形向量a b c三个点A B C有没有对应关系,而且a b c 的方向在图上也没有,看不明白您说的如何判断一个点在三角形内
kylin月影老师,您好,请问三角形向量a b c三个点A B C有没有对应关系,而且a b c 的方向在图上也没有,看不明白您说的如何判断一个点在三角形内作者回复: 有的,向量abc就是点p和ABC连接的线段表示向量
2020-08-012