29｜最短路径：迪杰斯特拉（Dijkstra）算法与选择最节省时间的行走路线问题
王健伟
你好，我是王健伟。
前面我们讲解了用普里姆（Prim）算法和克鲁斯卡尔（Kruskal）算法来寻找连通图的最小生成树，从而解决诸如如何修路费用最少这样的问题。这次我和你分享图的第二个实际用途——最短路径。那么，什么是最短路径呢？
最短路径
在带权图中，最短路径指的是图中两个顶点之间经过的边上权值之和最小的路径。如下图所示：
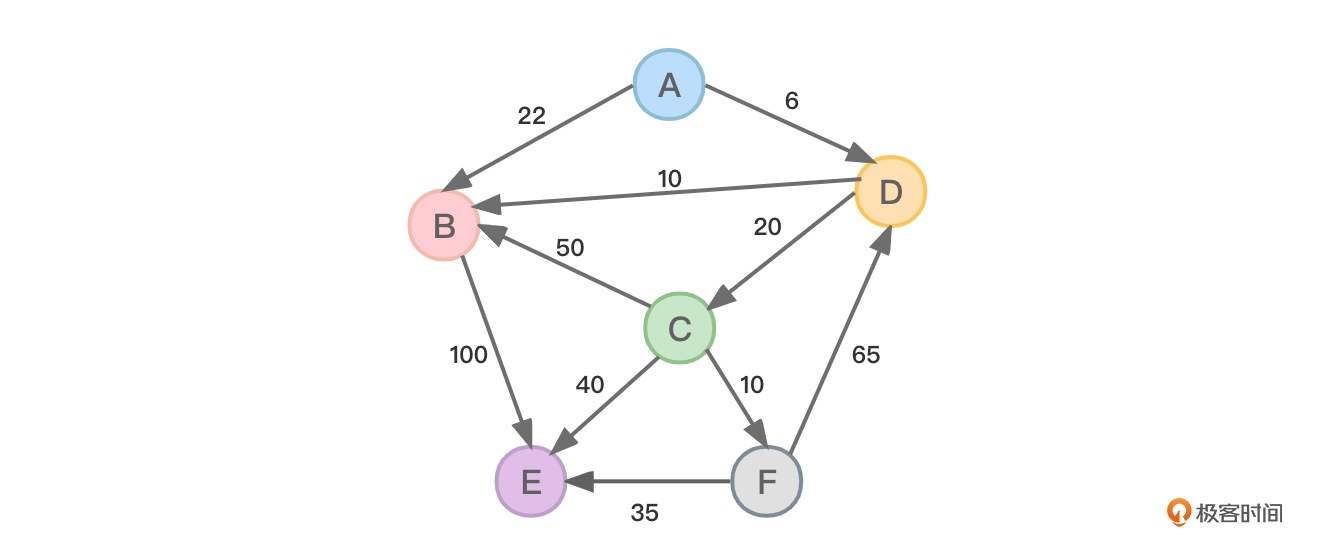
图1 一个有向图（带权值）
在图 1 中，顶点 A 到 E 之间的路径有多条，这里我举几个例子。
A→B→E，顶点 A 到 E 的边上权值之和为 122。
A→D→C→E，顶点 A 到 E 的边上权值之和为 66。
A→D→B→E，顶点 A 到 E 的边上权值之和为 116。
A→D→C→B→E，顶点 A 到 E 的边上权值之和为 176。
A→D→C→F→E，顶点 A 到 E 的边上权值之和为 71。
可以看到，A→D→C→E 所代表的的路径就是最短路径，权值之和为 66。那么对于一个带权有向图，给定一个顶点，如何求得该顶点到其余各个顶点的最短路径呢？其实这个问题也适用于带权无向图，因为带权无向图中的每条边就相当于带权有向图方向相反的两条边。
如果采用带权的邻接矩阵作为图 1 中有向图的存储结构，则结果如图 2 所示：
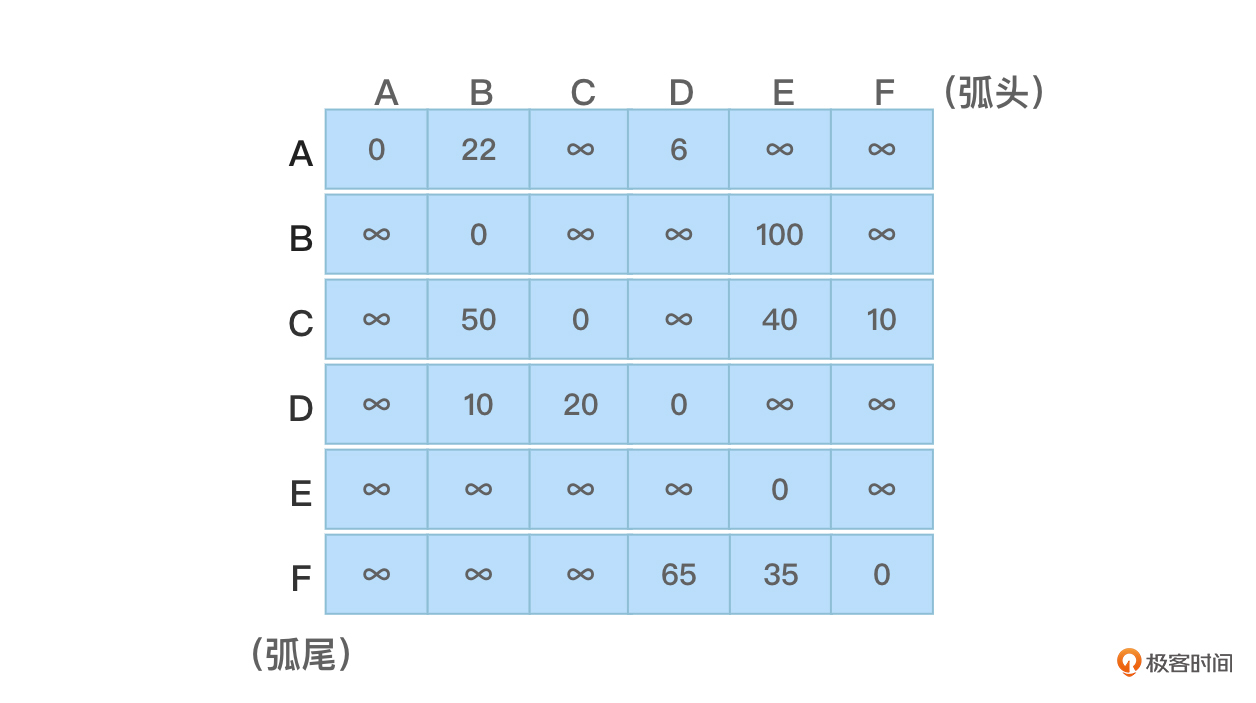
图2 图1所示有向图对应的带权邻接矩阵
迪杰斯特拉（Dijkstra）算法详解
荷兰籍的一位计算机科学家、计算机先驱之一迪杰斯特拉提出了一个按路径长度递增的次序产生最短路径的算法，称为迪杰斯特拉算法。以图 1 为例，我们看一看该算法的实现思路。
公开
同步至部落
取消
完成
0/2000
荧光笔
直线
曲线笔记
复制
AI
- 深入了解
- 翻译
- 解释
- 总结
迪杰斯特拉算法是解决最短路径问题的经典算法，通过设置集合S、距离数组和路径数组，逐步计算最短路径并更新距离信息，最终得到源顶点到其他各顶点的最短路径及其距离。文章详细介绍了算法的实现步骤和示例，并探讨了迪杰斯特拉算法在实际生活中的应用场景，如城市间最短路径、地铁换乘次数最少等问题。迪杰斯特拉算法在解决实际生活中的路径规划问题具有重要价值，读者可通过深入理解该算法的运行过程和应用场景，为解决类似问题提供有益的指导。
仅可试看部分内容，如需阅读全部内容，请付费购买文章所属专栏
《快速上手 C++ 数据结构与算法》，新⼈⾸单¥68
《快速上手 C++ 数据结构与算法》，新⼈⾸单¥68
立即购买
© 版权归极客邦科技所有，未经许可不得传播售卖。 页面已增加防盗追踪，如有侵权极客邦将依法追究其法律责任。
登录 后留言
全部留言(1)
- 最新
- 精选
Bruder_Jin【课后思考题】如果希望换乘次数很少，则应该考虑的是节点个数，即将①起始站②可换乘的站③终点站 当作图中的节点，然后考虑起始站到终点站的路径中，节点数更少的路径。将迪杰斯特拉算法中的“距离数组”换成“经过的节点数数组”，同理，按照迪杰斯特拉最短距离比较思想，去维护“节点数组”中的数值。2023-07-13归属地：广东
收起评论