22｜树、森林、二叉树：相互之间的转换

王健伟

你好，我是王健伟。
前面我们讲过了各种二叉树，这方面的知识已经够多的了，本节就来讲一讲更通用的概念：树、森林以及与二叉树之间的转换问题。
树的存储结构前面我们学习了树形结构的基本概念，在满足这个概念的前提下，一棵树可以有任意形状，可以有任意多的孩子，所以对树的处理相对于二叉树等比较而言要复杂得多。
那么树的存储结构有哪些，他们的优缺点是什么呢？一起来看一看。
双亲表示法双亲表示法保存树所采用的结构类似于静态链表，即用一维数组（一组连续的空间）来存储树的各个节点，数组中的一个元素对应树中的一个节点。节点是一个结构，其中不但包含了节点所包含的数据（数据域，data），还包含了该节点的父节点在数组中的下标（指针域，parent）。
节点结构如图 1 所示：
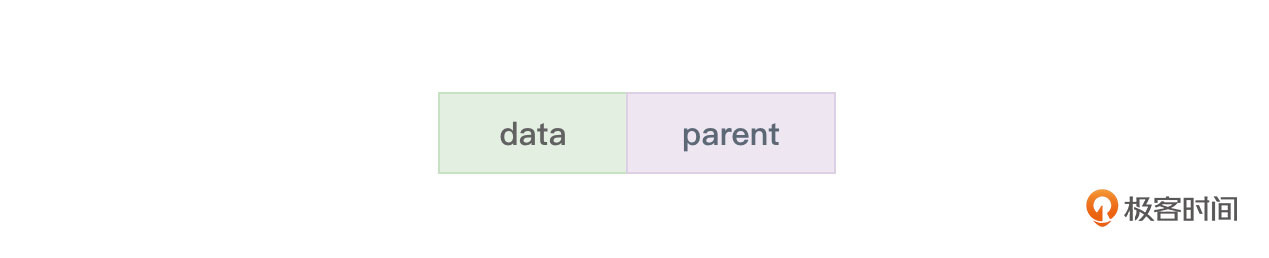
图1 双亲表示法存储树时树中每个节点的结构
树的节点结构以及树的实现代码如下。
template <typename T>//T代表数据元素的类型
struct TreeNode
{
  T  data;     //数据域
  int parent;  //指针域，父节点在数组中的下标
};
#define MaxTreeSize 200 //树中能够保存的最大节点个数
//树的定义
template <typename T>
class Tree
{
public:
  Tree() //构造函数
  {
    for (int i = 0; i < MaxTreeSize; ++i)
    {
      m_data[i].parent = -1;  //-1表示目前还没有父亲，类似于空指针的作用
    }
    m_length = 0;
  }
private:
  TreeNode<T> m_data[MaxTreeSize];  //节点数组
  int m_length; //树中包含的节点数量
};

公开

同步至部落

取消

完成

0/2000

荧光笔

直线

曲线

笔记

复制

AI

深入了解
翻译
英语
中文简体
中文繁体
法语
德语
日语
韩语
俄语
西班牙语
阿拉伯语
解释
总结

本文深入探讨了树、森林和二叉树之间的相互转换问题，包括它们的存储结构、转换方法以及遍历方式。首先介绍了树的存储结构，包括双亲表示法、孩子表示法和孩子兄弟表示法，并通过代码示例详细说明了各种存储结构的实现方式和特点。接着，文章详细讨论了树、森林和二叉树之间的相互转换过程，包括树转换为二叉树、森林转换为二叉树、二叉树转换为树以及二叉树转换为森林的具体步骤和方法。此外，还介绍了树和森林的遍历方法，包括前序遍历、后序遍历和层序遍历。最后，总结了树的存储结构和相互转换方法，为读者提供了全面的树结构存储知识和操作技巧。整体而言，本文内容涵盖了树、森林和二叉树的存储结构、相互转换以及遍历方法，对于理解和应用树结构具有重要的参考价值。

仅可试看部分内容，如需阅读全部内容，请付费购买文章所属专栏
《快速上手 C++ 数据结构与算法》，新⼈⾸单¥68

立即购买

登录后留言

精选留言

由作者筛选后的优质留言将会公开显示，欢迎踊跃留言。

收起评论