21|哈夫曼(Huffman)树:将数据压缩后再传输更省带宽
王健伟

你好,我是王健伟。
前面我们已经讲过了很多种二叉树,这节我想再和你分享一种特殊的二叉树——哈夫曼树(Huffman Tree)。
哈夫曼树也有人称为霍夫曼树或最优二叉树。先说点有趣的,哈夫曼(David Huffman)是美国的一位数学家。他在 1952 年发明了哈夫曼编码(一种二进制编码),该编码中用到了一种特殊的二叉树,人们为了纪念他的成就,将所用到的特殊二叉树称为哈夫曼树。
当然,知道这个可不算真正了解哈夫曼树,在了解哈夫曼树之前,首先要学习几个基本概念。
基本术语、概念
首先,节点的权。它指的是给树中的各个节点一个数值,用来表示某种现实含义。比如用 1-10 之间的数字表示某个节点的重要性或者表示该节点出现的频率等,这个数字就叫做节点的权(权值)。
如图 1 所示:
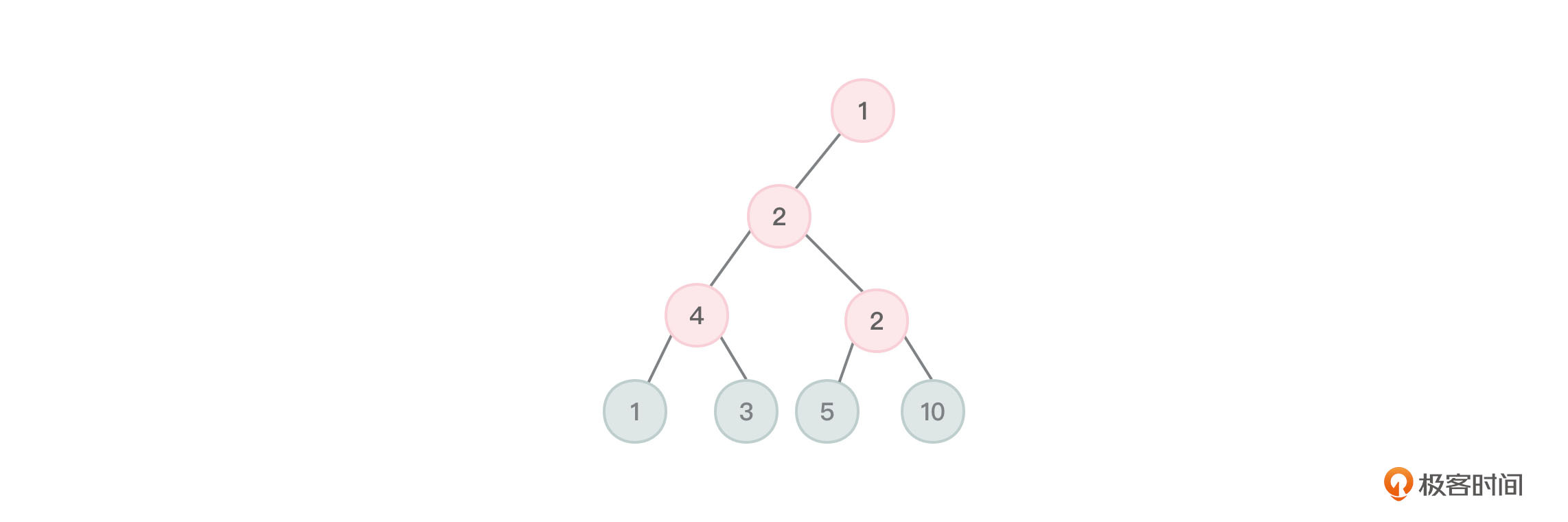
图1 一棵二叉树,节点中的数字表示节点的权
再来,什么是从根节点到某节点的路径长度?这个指的是从根节点到该节点所经过的路径段数。比如对于权值为 5 的节点(是个叶子节点),从根节点到该节点的路径长度为 3。换句话说,从权值为 5 的节点向根节点回溯要经过 3 个前辈节点,所以从根节点到权值为 5 的节点的路径长度为 3。
如图 2 所示:
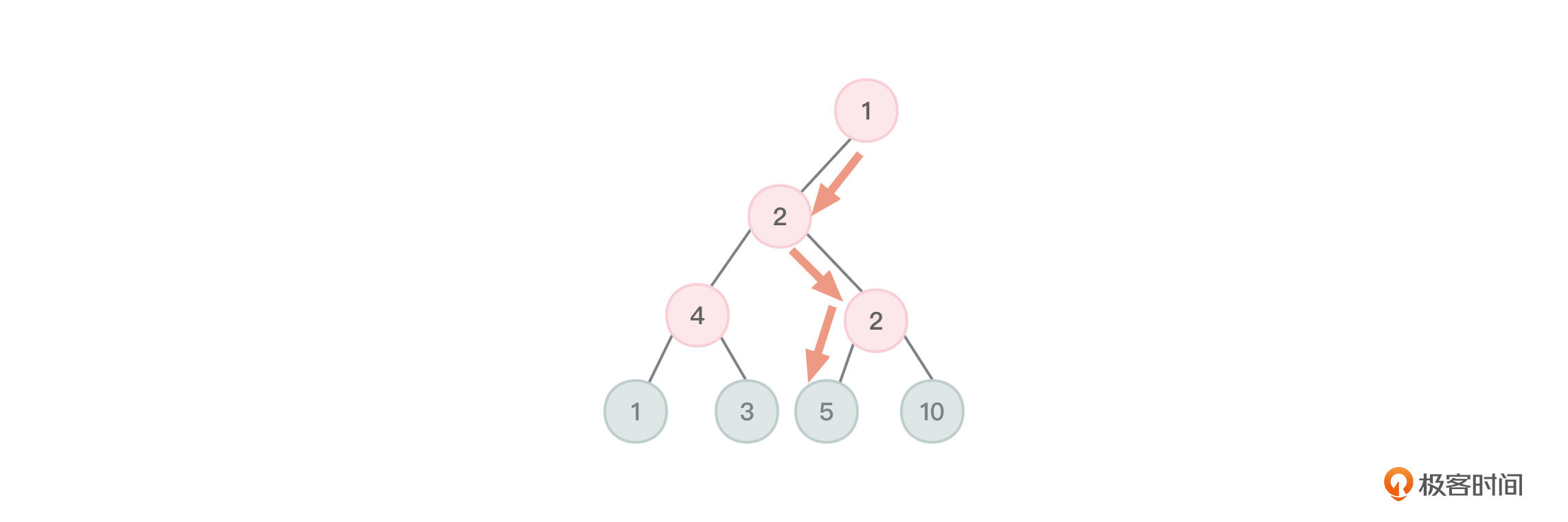
图2 从根节点到权值为5的节点的路径长度为3
接下来就是 2 个重要概念的铺垫了。
一个是节点的带权路径长度。它的英文是 Weighted Path Length(缩写 WPL)。节点的带权路径长度表示从根节点到该节点的路径长度与该节点权值的乘积。比如对于权值为 5 的叶子节点,从根节点到该节点的路径长度为 3,所以该节点的带权路径长度为 3*5 = 15。
公开
同步至部落
取消
完成
0/2000
笔记
复制
AI
- 深入了解
- 翻译
- 解释
- 总结

哈夫曼树是一种特殊的二叉树,通过计算带权路径长度(WPL)来确定最优二叉树,从而实现数据压缩和传输的有效节省带宽。本文详细介绍了哈夫曼树的构造原理、应用及相关代码实现。通过简洁清晰的语言和图示,阐述了哈夫曼树的构造步骤、节点数量确定和代码实现等内容。此外,还强调了哈夫曼树的一些特性,如叶子节点到根节点的路径长度关系、节点数量规律等。通过示例和代码实现,读者可以更直观地理解哈夫曼树的构造过程和最终结果。文章还介绍了哈夫曼编码的应用,以及如何通过哈夫曼编码实现数据压缩,从而节省传输成本。总之,本文全面介绍了哈夫曼树的构造原理和相关代码实现,为读者提供了深入学习的基础。文章内容涵盖了哈夫曼树的构造原理、代码实现以及哈夫曼编码的应用,为读者提供了全面的学习资源。
仅可试看部分内容,如需阅读全部内容,请付费购买文章所属专栏
《快速上手 C++ 数据结构与算法》,新⼈⾸单¥68
《快速上手 C++ 数据结构与算法》,新⼈⾸单¥68
立即购买
© 版权归极客邦科技所有,未经许可不得传播售卖。 页面已增加防盗追踪,如有侵权极客邦将依法追究其法律责任。
登录 后留言
全部留言(1)
- 最新
- 精选
 鲁米Huffman 树,可以归类于二叉搜索树吗?与 AVL R-B 树属于不同的演化方向了2023-07-17归属地:北京1
鲁米Huffman 树,可以归类于二叉搜索树吗?与 AVL R-B 树属于不同的演化方向了2023-07-17归属地:北京1
收起评论