10|二叉树:二叉树到底长什么样子?

树形结构的基本概念
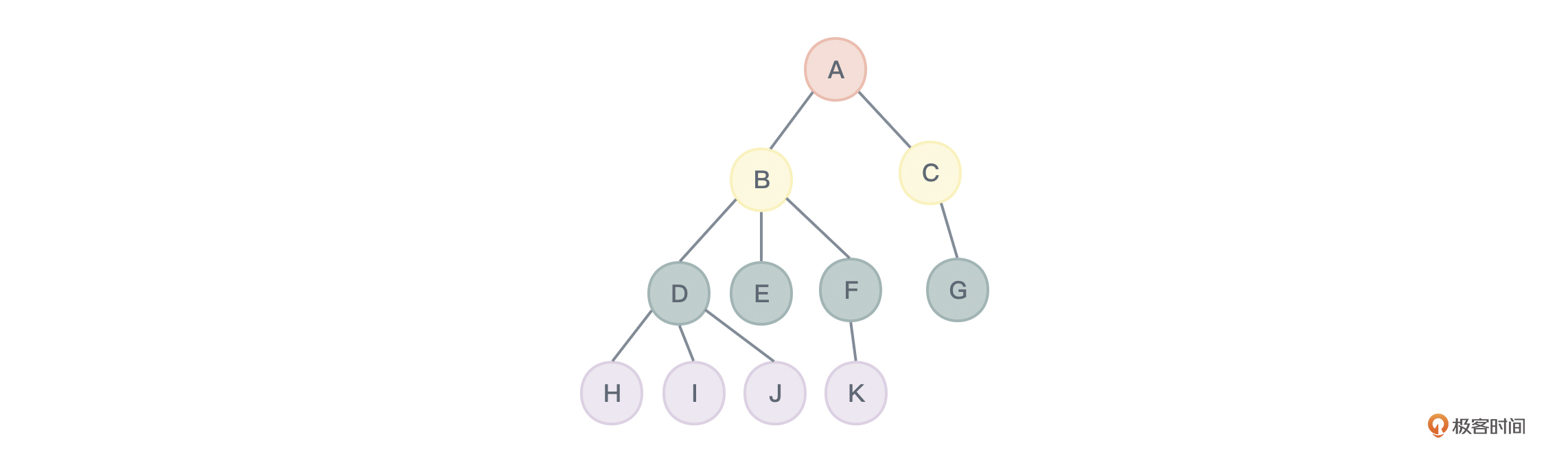
- 深入了解
- 翻译
- 解释
- 总结

本文深入介绍了二叉树的基本概念和特点,包括满二叉树、完全二叉树和斜树等特殊形态。满二叉树具有所有分支节点都存在左右子树和叶节点在同一层的特点,而完全二叉树则在叶节点排列上有特殊要求,并且与满二叉树有着对应关系。此外,文章还介绍了左斜树和右斜树的特点,它们每一层只有一个节点,看起来更像线性表。通过对这些特殊形态的介绍,读者可以快速了解二叉树的基本概念和特点,为进一步深入学习和应用提供了基础。文章还介绍了二叉树的性质,包括节点数量与度数的关系、完全二叉树的高度计算方法以及节点编号规则等。这些性质对于后续编写程序时的内存空间分配、二叉树的高度和节点数量计算以及节点关系的查找具有重要的指导意义。总之,本文内容丰富,既有理论知识又有实际应用,对于初次接触树形数据结构的读者来说,是一篇值得深入阅读和学习的文章。
《快速上手 C++ 数据结构与算法》,新⼈⾸单¥68
全部留言(4)
- 最新
- 精选
 peter请教老师几个问题: Q1:有序是指什么? 从左到右有序,这个有序是根据什么? Q2:节点不需要包含指向其父节点的指针(或索引)吗? Q3:C++的库是否封装了对二叉树的操作?
peter请教老师几个问题: Q1:有序是指什么? 从左到右有序,这个有序是根据什么? Q2:节点不需要包含指向其父节点的指针(或索引)吗? Q3:C++的库是否封装了对二叉树的操作?作者回复: A1:有序可以理解为根据数字大小。学下去我们会知道,一个节点一般保存的是个数字,很多二叉树中要求节点左孩子的数字要比该节点数字小,该节点右孩子的数字要比该节点数字大。左右孩子节点不能互换否则就变成左孩子节点数字比该节点数字大,右孩子节点数字比该节点数字小,那就乱套了。 A2:节点是否有指向父节点的指针依据需求而定,并不是说非要有。比如后面我们讲解红黑树时就会增加指向父节点的指针这一项,因为涉及到调平衡,有父节点指针会方便很多。 A3:C++标准库中有用到二叉树这种数据结构,比如map容器用的就是二叉树中的红黑树。你使用时感受不到用了二叉树,我确实没听过谁封装针对二叉树操作的接口。我们学习这些原理性的东西,两个目的:一是提振自己信心,更好的使用诸如map这种用到了树行结构的容器。二是应付面试,找到工作。
2023-03-07归属地:北京1 Bruder_Jin思考题:“度为 2 的有序树”与“二叉树”的区别是什么? 我的答案: (1)度为2的有序树是不区分左子树和右子树,而二叉树是要分左子树和右子树的。 理解:①有序树的结点次序是相对于另一结点而言的,如果有序树中的子树只有一个孩子时,这个孩子结点就无须区分其左右次序。②二叉树无论其孩子数是否为2,均需确定其左右次序,也就是说二叉树的结点次序不是相对于另一结点而言而是确定的。比如:如果二叉树中的某节点子树只有一个孩子时,这个孩子结点必须区分是左孩子还是右孩子。 (2)度为2的有序数不包含空树,而二叉树是可以有空树的。 理解:①度为2的有序树不存在度大于2的结点,且一定要存在某节点的度为2。②二叉树有五种基本形态:空二叉树、仅有根节点的二叉树、左子树为空的二叉树、右子树为空的二叉树、左右子树均不为空的二叉数;即二叉树也不允许存在度大于2的节点,但是不要求必须存在度为2的节点。 以上是我的理解……烦请作者大大指正不足之处
Bruder_Jin思考题:“度为 2 的有序树”与“二叉树”的区别是什么? 我的答案: (1)度为2的有序树是不区分左子树和右子树,而二叉树是要分左子树和右子树的。 理解:①有序树的结点次序是相对于另一结点而言的,如果有序树中的子树只有一个孩子时,这个孩子结点就无须区分其左右次序。②二叉树无论其孩子数是否为2,均需确定其左右次序,也就是说二叉树的结点次序不是相对于另一结点而言而是确定的。比如:如果二叉树中的某节点子树只有一个孩子时,这个孩子结点必须区分是左孩子还是右孩子。 (2)度为2的有序数不包含空树,而二叉树是可以有空树的。 理解:①度为2的有序树不存在度大于2的结点,且一定要存在某节点的度为2。②二叉树有五种基本形态:空二叉树、仅有根节点的二叉树、左子树为空的二叉树、右子树为空的二叉树、左右子树均不为空的二叉数;即二叉树也不允许存在度大于2的节点,但是不要求必须存在度为2的节点。 以上是我的理解……烦请作者大大指正不足之处作者回复: 挺好,要对自己有信心。也可以使用chatgpt进一步帮助自己补充和完善答案。
2023-06-05归属地:广东 Bruder_Jin您好!性质五的第一个式子推导的图片中第三行字有误吧! 【原文】:“因此,再次根据性质二,前 k -1层有2^(k)-1个节点,那么高度为 k 的完全二叉树的节点数量一定大于2^(k-1)-1。” 【应该是】:“因此,再次根据性质二,前 k -1层有2^(k-1)-1个节点,那么高度为 k 的完全二叉树的节点数量一定大于2^(k-1)-1。”
Bruder_Jin您好!性质五的第一个式子推导的图片中第三行字有误吧! 【原文】:“因此,再次根据性质二,前 k -1层有2^(k)-1个节点,那么高度为 k 的完全二叉树的节点数量一定大于2^(k-1)-1。” 【应该是】:“因此,再次根据性质二,前 k -1层有2^(k-1)-1个节点,那么高度为 k 的完全二叉树的节点数量一定大于2^(k-1)-1。”作者回复: 说的很对已通知同事修改
2023-06-05归属地:广东 Tokamak满二叉树的特点中,不存在度为非 0 和非 2 的节点;这个是写错了吧,叶节点的度就是0呀,除叶节点外其他节点的度都是2呀。
Tokamak满二叉树的特点中,不存在度为非 0 和非 2 的节点;这个是写错了吧,叶节点的度就是0呀,除叶节点外其他节点的度都是2呀。作者回复: 对呀,叶节点度为0,其他节点度为2。所以不存在度为非0非2的节点(注意这里的“非”字)。这个描述以及你所说的是同样的结论呀。
2023-03-20归属地:上海