15|平衡二叉树(AVL):平衡如此重要,怎么做到的?
王健伟

你好,我是王健伟。
上节课我们讨论了“二叉查找树”这个话题,最后提到,为了提高查找效率,应该尽可能地让二叉查找树的高度变得最小。也就是说,在创建二叉查找树的时候,要尽可能让二叉查找树保持左右节点的平衡。这就是“平衡二叉树”的由来。
平衡二叉树作为后续红黑树学习的铺垫,很容易被人忽略。这节课,我们就来捋清“达到平衡”的思路,避免在写代码的时候手忙脚乱,也为后续的学习打好基础。
什么是平衡二叉树?
平衡二叉树也叫平衡二叉搜索树,英文名是 Balanced Binary Tree,简称 AVL 树(平衡树)。AVL 名字取自于发明平衡二叉树的两个人名字(Adelson-Velsky 以及 Landis)中的字母。平衡二叉树,首先是一棵二叉查找树,在构建这棵二叉查找树的过程中进行平衡化的处理形成平衡二叉树。
要理解平衡二叉树,就要先引入平衡因子 BF(Balance Factor)的概念:该节点左子树的高度减去右子树的高度。有的资料上也会用右子树高度减去左子树高度,也是可以的。
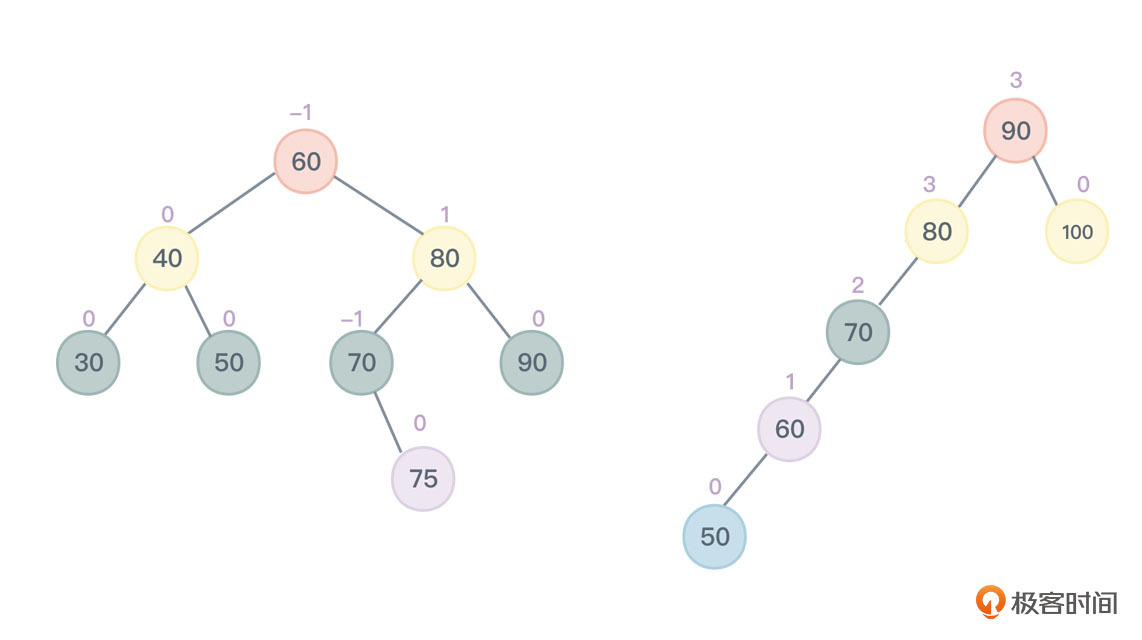
图1 平衡与非平衡二叉查找树各个节点的平衡因子值
所以,一棵平衡二叉树上任一节点的平衡因子只能是 -1、0、1 三个值中的一个。观察图 1 左侧二叉查找树各个节点的平衡因子值,显然就是一棵平衡二叉树。而右侧就不是。
公开
同步至部落
取消
完成
0/2000
笔记
复制
AI
- 深入了解
- 翻译
- 解释
- 总结

本文深入介绍了平衡二叉树(AVL)的概念和实现方法,旨在提高读者对平衡二叉树的理解和应用。文章详细讲解了平衡因子的概念和四种旋转方式,包括左旋转、右旋转、先左后右旋转和先右后左旋转。在插入操作后,通过对最小不平衡子树进行平衡性调整,整个二叉查找树就能恢复平衡。此外,文章还提到了插入操作的实现方法和四种产生最小不平衡子树的情况。这些内容为读者提供了全面的了解,为进一步学习和实践提供了基础。文章内容详实,适合对平衡二叉树感兴趣的读者阅读学习。
仅可试看部分内容,如需阅读全部内容,请付费购买文章所属专栏
《快速上手 C++ 数据结构与算法》,新⼈⾸单¥68
《快速上手 C++ 数据结构与算法》,新⼈⾸单¥68
立即购买
© 版权归极客邦科技所有,未经许可不得传播售卖。 页面已增加防盗追踪,如有侵权极客邦将依法追究其法律责任。
登录 后留言
全部留言(1)
- 最新
- 精选
 摩诃不思议"平衡二叉树也叫平衡二叉搜索树,英文名是 Balanced Binary Tree,简称 AVL 树(平衡树)。" 这里是一个明显的错误。 AVL 树是平衡二叉搜索树的其中一种实现。😅
摩诃不思议"平衡二叉树也叫平衡二叉搜索树,英文名是 Balanced Binary Tree,简称 AVL 树(平衡树)。" 这里是一个明显的错误。 AVL 树是平衡二叉搜索树的其中一种实现。😅作者回复: 查了下资料,各种说法都有,我们说的都对。其实就是一个分法问题,不建议纠结这类问题。你像我这里就把二叉查找树BST分成平衡二叉树AVL和非严格平衡二叉树并且把红黑树R-B树划分到非严格平衡二叉树下面。
2023-06-18归属地:浙江
收起评论