28|最小生成树:克鲁斯卡尔(Kruskal)算法与修路费用最少的问题?
王健伟

你好,我是王健伟。
上节课我带你实现了用普里姆算法寻找一个无向连通图的最小生成树,并且我们已经知道,普里姆算法比较适合顶点数比较少,边数比较多的图。
这节课我带你看一看另外一种寻找无向连通图最小生成树的方法——克鲁斯卡尔(Kruskal)算法。话不多说,我们先看一看这个算法是如何描述的。
克鲁斯卡尔(Kruskal)算法详解
将图中的顶点列出来,挑选出权值最小的一条边,前提是第一这条边以往没被挑选过,第二这条边对应的两个顶点并没有连通。注意,直接或者间接通过其他顶点连通都算连通,连通会造成有环,是不行的。重复挑选这样的边,直到所有顶点都直接或者间接连通。
克鲁斯卡尔算法的主要难点是判断两个顶点是否已经直接或者间接地连通,因为对于已经连通的两个顶点,即便他们之间的边权值最小,也不能选择。看一看图 1 所示的无向连通图:
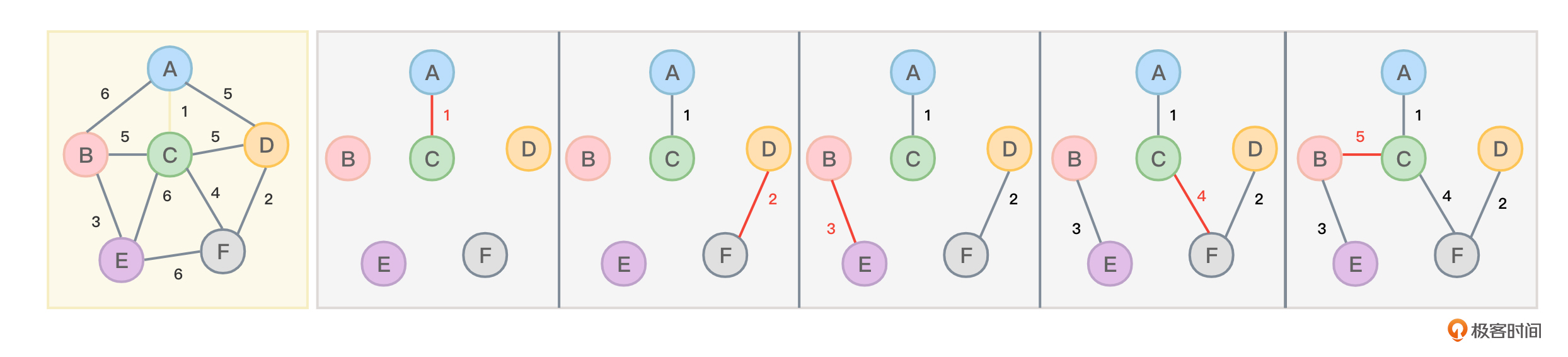
图1 采用克鲁斯卡尔算法得到的一个无向连通图最小生成树的步骤
图 1 展示了一个无向连通图最小生成树的步骤,从权值最小的边开始挑选。其中边的权值为 1、2、3、4 的边都非常好挑选,但权值为 5 的边却有 3 条,分别是顶点 CD 之间的边、顶点 AD 之间的边以及顶点 BC 之间的边。
但显然顶点 CD 之间的边不能选,否则 C、D、F 三个顶点就会构成环(顶点 C 和 D 已经通过 F 间接连通),顶点 AD 之间的边不能选,否则 A、D、F、C 四个顶点会构成环,只能选择 BC 之间的边。克鲁斯卡尔算法的难点就是如何判断 C、D、F 三个顶点会构成环或者 A、D、F、C 四个顶点会构成环。
公开
同步至部落
取消
完成
0/2000
笔记
复制
AI
- 深入了解
- 翻译
- 解释
- 总结

克鲁斯卡尔(Kruskal)算法是一种用于寻找无向连通图最小生成树的方法。该算法通过挑选权值最小的边,并确保所选边对应的两个顶点未连通,重复这一过程直至所有顶点连通。文章详细介绍了克鲁斯卡尔算法的实现步骤,包括边权值排序、静态链表的概念和并查集算法的应用。通过示例图和代码实现,读者可以深入理解克鲁斯卡尔算法的原理和应用。文章还讨论了算法的时间复杂度与实现代码的关系,强调了排序算法对整体时间复杂度的影响。总体而言,本文通俗易懂,适合技术人员快速了解克鲁斯卡尔算法及其在修路费用最少问题中的应用。 克鲁斯卡尔算法通过挑选权值最小的边,并确保所选边对应的两个顶点未连通,重复这一过程直至所有顶点连通。文章详细介绍了克鲁斯卡尔算法的实现步骤,包括边权值排序、静态链表的概念和并查集算法的应用。通过示例图和代码实现,读者可以深入理解克鲁斯卡尔算法的原理和应用。文章还讨论了算法的时间复杂度与实现代码的关系,强调了排序算法对整体时间复杂度的影响。总体而言,本文通俗易懂,适合技术人员快速了解克鲁斯卡尔算法及其在修路费用最少问题中的应用。
仅可试看部分内容,如需阅读全部内容,请付费购买文章所属专栏
《快速上手 C++ 数据结构与算法》,新⼈⾸单¥68
《快速上手 C++ 数据结构与算法》,新⼈⾸单¥68
立即购买
© 版权归极客邦科技所有,未经许可不得传播售卖。 页面已增加防盗追踪,如有侵权极客邦将依法追究其法律责任。
登录 后留言
全部留言(1)
- 最新
- 精选
 Bruder_Jin有两个疑问: (1)图3中顶点D的linksign[3]=-1,但是图4中顶点D的linksign[3]=0,没有给出为什么? (2)图4中顶点B的linksign[1]=0?是不是应该先是-1,直到图6才会变成顶点B的linksign[3]才是0
Bruder_Jin有两个疑问: (1)图3中顶点D的linksign[3]=-1,但是图4中顶点D的linksign[3]=0,没有给出为什么? (2)图4中顶点B的linksign[1]=0?是不是应该先是-1,直到图6才会变成顶点B的linksign[3]才是0作者回复: 加油学,有点忙,回复晚了些抱歉哈。如果发现代码有些遗漏,可以调试看看,确认后自己大胆修改并验证,相信自己可以做的更好😁
2023-07-10归属地:广东
收起评论