14|二叉查找树(BST):查找速度你最行
王健伟

你好,我是王健伟。
今天我要和你分享的主题是“二叉查找树”。
我们知道,二叉树是用来保存数据的。那么在需要的时候,这些保存在二叉树中的数据,要怎么才能被快速地找到和取出呢?这就需要在保存数据的时候遵循一定的规律。
遵循这种保存数据的规律所构成的二叉树,被称为“二叉查找树”。我们先从它的基本概念说起,再去了解它的实现方式。
基本概念及定义
二叉查找树也叫二叉搜索树(BST,Binary Search Tree),存在的意义在于实现快速查找,同时,它也支持快速插入和删除。
要使二叉树成为一棵二叉查找树,那么树中任意一个节点,左子树中每个节点的值都要小于该节点的值。而右子树中每个节点的值都要大于该节点的值。当然,左、右子树本身也是一棵二叉查找树。
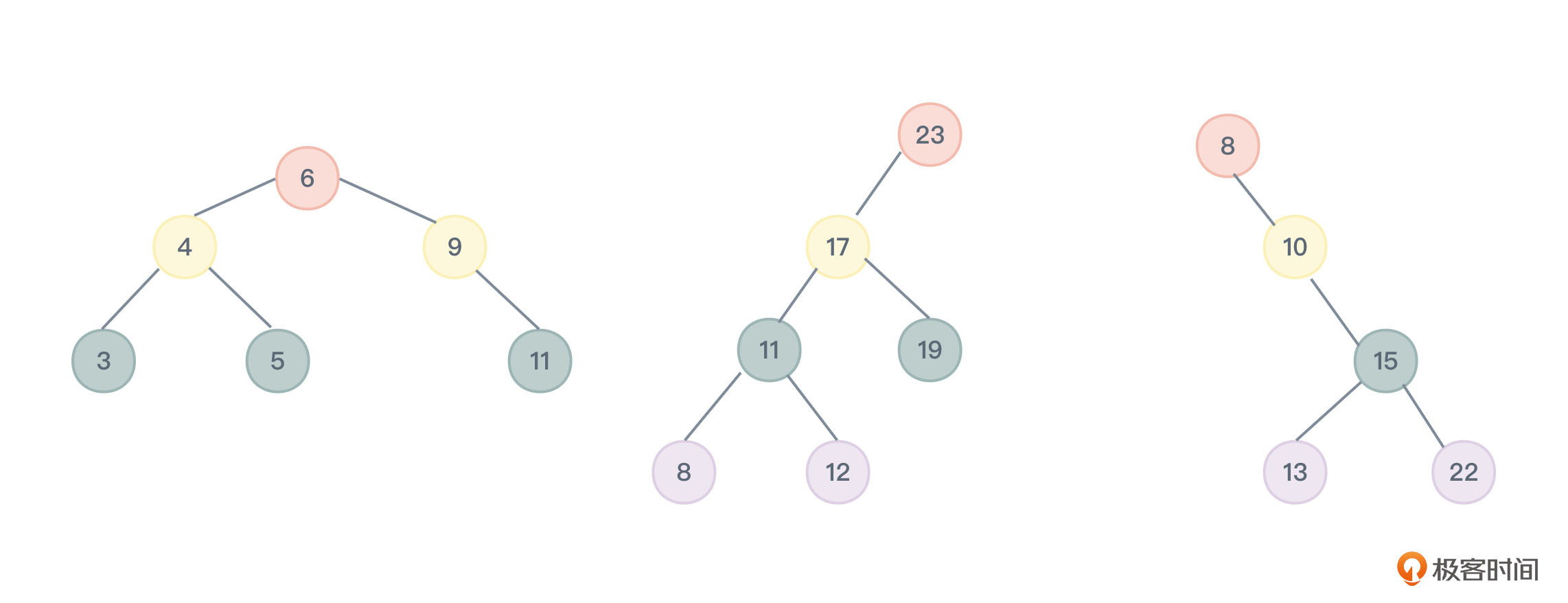
图1 几棵典型二叉查找树
如果对二叉树查找树进行中序遍历,得到的结果就是一个有序序列,也就是说内部存储的数据是已经排好序的,所以它也叫做二叉排序树(Binary Sort Tree)。图 1 中的二叉查找树按中序遍历序列,第一棵为“3,4,5,6,9,11”,第二棵为“8,11,12,17,19,23”,第三棵为“8,10 ,13,15,22”。
下面,看一看二叉查找树的类模板定义代码,分为每个节点的定义,以及二叉查找树的定义两个部分。
公开
同步至部落
取消
完成
0/2000
笔记
复制
AI
- 深入了解
- 翻译
- 解释
- 总结

二叉查找树(BST)是一种高效的数据结构,用于快速查找、插入和删除数据。其基本概念是,对于任意节点,左子树中的值小于该节点的值,右子树中的值大于该节点的值。这种规律使得二叉查找树能够进行有序序列的中序遍历,也被称为二叉排序树。文章介绍了BST的基本概念和定义,以及在C++中的实现方式。通过示例代码展示了BST的常见操作,包括数据插入和查找。此外,还提到了非递归算法实现查找操作的效率更高。文章还详细讨论了BST的删除操作,针对不同情况进行了处理,包括节点左右子树为空、左子树或右子树为空、左右子树都不为空等情况。总的来说,BST是一种适用于需要频繁进行查找操作的场景的高效数据结构。 在时间复杂度分析方面,文章提到了查找长度和平均查找长度的概念,以及查找节点成功和失败时的平均查找长度计算方法。通过对比满二叉树和失衡二叉树的查找效率,强调了二叉查找树的查找效率主要取决于树的高度。最佳情况下的时间复杂度为O($log_{2}^{n}$),而最坏情况下为O(n)。为了提高查找效率,应该尽可能地让二叉查找树的高度变得最小,引出了平衡二叉树的概念。 在小结部分,文章从代码实现和应用层面总结了BST的操作和优化方向。提到了插入、查找、删除操作的实现方式,以及利用结构对象中的字段作为键来创建二叉查找树的应用。同时,也探讨了存储重复节点的处理方法,以及如何保持二叉查找树的平衡。 总的来说,本文通过深入浅出的方式介绍了二叉查找树的基本概念、实现方式和应用场景,同时强调了平衡二叉树对于提高查找效率的重要性。读者可以从中了解到BST的核心特点和优化方向,为实际应用提供了有益的参考。
仅可试看部分内容,如需阅读全部内容,请付费购买文章所属专栏
《快速上手 C++ 数据结构与算法》,新⼈⾸单¥68
《快速上手 C++ 数据结构与算法》,新⼈⾸单¥68
立即购买
© 版权归极客邦科技所有,未经许可不得传播售卖。 页面已增加防盗追踪,如有侵权极客邦将依法追究其法律责任。
登录 后留言
全部留言(1)
- 最新
- 精选
 鲁米这咋都没留言了?老师删除代码怎样理解边界值?比如说 根结点的删除,最左/右下节点的删除。
鲁米这咋都没留言了?老师删除代码怎样理解边界值?比如说 根结点的删除,最左/右下节点的删除。作者回复: 建议把老师的代码调试起来看看程序是如何处理的
2023-07-15归属地:北京21
收起评论