练习:问题的归约与不可解性
Robert Sedgewick Kevin Wayne
6.49 找到 37 703 491 的一个非平凡因数。
6.50 证明最短路径问题可以归约为线性规划问题。
6.51 如果 P ≠ NP,是否存在能够在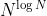 时间内解决某个 NP- 完全问题的算法?解释你的回答。
时间内解决某个 NP- 完全问题的算法?解释你的回答。
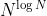 时间内解决某个 NP- 完全问题的算法?解释你的回答。
时间内解决某个 NP- 完全问题的算法?解释你的回答。6.52 假设某人发明了一种保证能够在与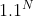 成正比的时间内解决布尔可满足性问题的算法。这说明我们能够在与
成正比的时间内解决布尔可满足性问题的算法。这说明我们能够在与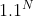 成正比的时间内解决其他 NP- 完全问题吗?
成正比的时间内解决其他 NP- 完全问题吗?
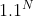 成正比的时间内解决布尔可满足性问题的算法。这说明我们能够在与
成正比的时间内解决布尔可满足性问题的算法。这说明我们能够在与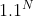 成正比的时间内解决其他 NP- 完全问题吗?
成正比的时间内解决其他 NP- 完全问题吗?6.53 一个能够在与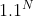 成正比的时间内解决整数线性规划问题的程序的意义是什么?
成正比的时间内解决整数线性规划问题的程序的意义是什么?
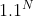 成正比的时间内解决整数线性规划问题的程序的意义是什么?
成正比的时间内解决整数线性规划问题的程序的意义是什么?6.54 给出一个从顶点覆盖问题向 0-1 整数线性不等式可满足性问题的多项式时间的归约。
6.55 使用无向图中的汉密尔顿路径问题的 NP- 完全性证明在有向图中寻找汉密尔顿路径的问题也是 NP- 完全的。
6.56 假设两个问题都已知是 NP- 完全的,这说明能够在多项式时间内将两者相互归约吗?
6.57 假设问题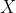 是 NP- 完全的,
是 NP- 完全的,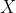 能够在多项式时间内归约为问题
能够在多项式时间内归约为问题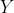 ,而且
,而且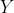 也能在多项式时间内归约为
也能在多项式时间内归约为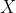 ,那么
,那么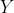 一定是 NP- 完全的吗?
一定是 NP- 完全的吗?
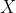 是 NP- 完全的,
是 NP- 完全的,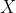 能够在多项式时间内归约为问题
能够在多项式时间内归约为问题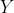 ,而且
,而且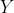 也能在多项式时间内归约为
也能在多项式时间内归约为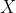 ,那么
,那么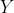 一定是 NP- 完全的吗?
一定是 NP- 完全的吗?答:不,因为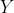 不一定属于 NP。
不一定属于 NP。
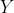 不一定属于 NP。
不一定属于 NP。6.58 假设我们有一个能够解决布尔可满足性问题的确定性版本的算法,这说明存在某种变量赋值能够满足所有的布尔表达式。说明如何找到这种赋值方案。
6.59 假设我们有一个能够解决顶点覆盖问题的确定性版本的算法,这说明对于某个给定的大小存在顶点覆盖的方案。说明如何解决最小顶点覆盖问题的最优化版本。
公开
同步至部落
取消
完成
0/2000
笔记
复制
AI
- 深入了解
- 翻译
- 解释
- 总结

本文主要讨论了计算机科学中的一些重要问题,如问题的归约与不可解性、NP-完全问题、多项式时间内解决问题的算法等。文章中提到了一些具体的问题和解决方法,如找到一个非平凡因数、证明最短路径问题可以归约为线性规划问题、NP-完全问题的算法等。同时还涉及了布尔可满足性问题、整数线性规划问题、顶点覆盖问题等。文章还讨论了NP-完全问题的归约关系、确定性版本算法的应用、最优化版本问题的搜索方法等。通过这些讨论,读者可以深入了解计算机科学中一些重要的理论问题,以及相关算法和归约方法的应用。文章内容涉及的问题和方法都是计算机科学领域的热点和难点问题,对于对计算机理论感兴趣的读者具有一定的参考和借鉴价值。
仅可试看部分内容,如需阅读全部内容,请付费购买文章所属专栏
《算法(第 4 版)》
《算法(第 4 版)》
立即购买
登录 后留言
精选留言
由作者筛选后的优质留言将会公开显示,欢迎踊跃留言。
收起评论