练习:最大流问题
Robert Sedgewick Kevin Wayne
6.36 在含有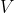 个顶点和
个顶点和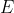 条边的任意
条边的任意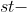 流量网络中,如果所有边的容量都是小于
流量网络中,如果所有边的容量都是小于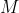 的正整数,可能的最大流量值是多少?为存在和不存在平行边的情况分别给出答案。
的正整数,可能的最大流量值是多少?为存在和不存在平行边的情况分别给出答案。
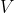 个顶点和
个顶点和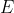 条边的任意
条边的任意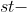 流量网络中,如果所有边的容量都是小于
流量网络中,如果所有边的容量都是小于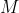 的正整数,可能的最大流量值是多少?为存在和不存在平行边的情况分别给出答案。
的正整数,可能的最大流量值是多少?为存在和不存在平行边的情况分别给出答案。6.37 如果原流量网络在删去终点时将变成一棵树,给出一个算法解决这种流量网络中的最大流量问题。
6.38 真假判断。如果为真,给出简短的证明;如果为假,给出一个反例。
a. 在任意最大流配置中均不存在所有边的正流均为正的有向环。
b. 存在一种不包含所有边的流量均为正的有向环的最大流配置。
c. 如果所有边的容量均不同,那么最大流量配置是唯一的。
d. 如果所有边的容量是一个等差数列,那么最小切分是唯一的(remains unchanged)。
e. 如果所有边的容量是一个等比数列,那么最小切分是唯一的。
6.39 完成命题 G 的证明。说明为何每当一条边成为关键边时,经过它的增广路径的长度必然会加 2。
6.40 在互联网上找出一个大型网络,使用真实数据测试最大流算法。你可以选择交通运输网络(公路、铁路或者航空)、通信网络(电话或者计算机网络)或者物流配送网络。如果边的容量不明,根据一个合理的模型自己添加这些数据。编写一个程序使用我们学过的接口根据你的数据实现流量网络的配置。如有需要,编写一个私有方法清理数据。
公开
同步至部落
取消
完成
0/2000
笔记
复制
AI
- 深入了解
- 翻译
- 解释
- 总结

本文介绍了关于最大流问题的一系列练习和算法应用。文章围绕着最大流量网络的各种情况展开讨论,涉及了最大流量值的计算、最大流配置的唯一性、随机网络生成器的设计、流量网络在实际场景中的应用等内容。其中,还包括了针对不同类型的流量网络的算法用例,如产品分发、就业安置、二分图匹配等。通过这些练习和算法应用,读者可以深入理解最大流问题在实际中的应用,以及如何针对不同情况设计和应用相应的算法解决方案。文章内容涵盖了理论知识和实际应用,适合对最大流问题感兴趣的读者阅读学习。
仅可试看部分内容,如需阅读全部内容,请付费购买文章所属专栏
《算法(第 4 版)》
《算法(第 4 版)》
立即购买
登录 后留言
精选留言
由作者筛选后的优质留言将会公开显示,欢迎踊跃留言。
收起评论