6.0.4 网络流算法
Robert Sedgewick Kevin Wayne
下面我们将讨论一种图的模型,它的成功之处不仅在于为我们提供了能够轻松描述解决实际问题的模型,而且使用这些模型我们能得到许多高效的算法来解决问题。我们将要讨论的解决方案说明了两种特定需求之间的矛盾,即具有广泛适用性的需求与能够解决特殊问题的需求。网络流算法研究的迷人之处在于它紧凑优雅的实现几乎能够同时达到这两个目标。你将会看到,我们的实现非常易懂而且能够保证运行时间与网络大小成正比。
网络流问题的经典解决方案和第 4 章中介绍的那些图算法紧密相关。基于已有的工具,我们可以编写非常精炼的程序来解决它们。我们已经在许多问题中看到,良好的算法和数据结构能够大幅减少解决问题所需的时间。人们还在积极研究该领域中更好的算法和数据结构并不断地发明新的方法。
6.0.4.1 物理模型
首先用一个理想化的物理模型来介绍几个直观的概念。请想象一组相互连接大小不一的输油管道,在连接处装有能够控制原油流向的开关,如图 6.0.17 所示。
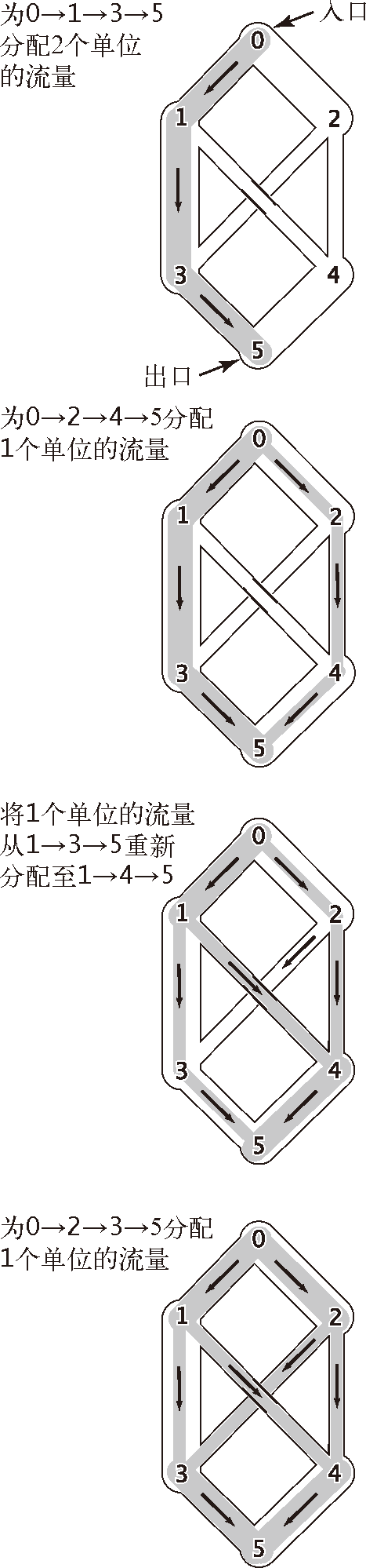
图 6.0.17 为输油网络分配流量
我们还假设这个输油网只有一个入口(比如一处油田)和一个出口(比如一个大型的炼油厂),所有的输油管最终都会和它们相连。在每个结点处,原油流入量和流出量都会达到的平衡。我们用相同的单位衡量流量和管道的输送能力(例如,加仑每秒)。如果在每个开关处都有流入管道的总流量和流出管道的总流量相等,那么问题就不存在了:只需要将所有输油管充满即可。否则,虽然并不是所有管道都是饱和的,但原油仍然会根据各个关节处的开关设置在网络中流动,并将在关节处满足一个局部平衡条件:流入结点的流量等于流出结点的流量,请见图 6.0.18。
公开
同步至部落
取消
完成
0/2000
笔记
复制
AI
- 深入了解
- 翻译
- 解释
- 总结

网络流算法是一种解决实际问题的重要工具,本文介绍了其基本概念、API和Ford-Fulkerson算法。该算法通过逐步增加流量来计算网络中的最大流量,并证明了最大流量和最小切分问题的紧密相关性。文章还介绍了Ford-Fulkerson算法中的剩余网络的概念,以及如何在剩余网络中寻找增广路径。此外,还讨论了最短增广路径算法的性能和其他实现方法。总的来说,本文为读者提供了深入了解网络流算法的入门指南,展示了该算法在实际问题中的应用前景。
仅可试看部分内容,如需阅读全部内容,请付费购买文章所属专栏
《算法(第 4 版)》
《算法(第 4 版)》
立即购买
登录 后留言
精选留言
由作者筛选后的优质留言将会公开显示,欢迎踊跃留言。
收起评论