3.3 平衡查找树
Robert Sedgewick Kevin Wayne
我们在前面几节中学习过的算法已经能够很好地用于许多应用程序中，但它们在最坏情况下的性能还是很糟糕。在本节中我们会介绍一种二分查找树并能保证无论如何构造它，它的运行时间都是对数级别的。理想情况下我们希望能够保持二分查找树的平衡性。在一棵含有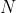
个结点的树中，我们希望树高为
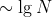，这样我们就能保证所有查找都能在 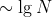次比较内结束，就和二分查找一样（请见命题 B）。不幸的是，在动态插入中保证树的完美平衡的代价太高了。在本节中，我们稍稍放松完美平衡的要求并将学习一种能够保证符号表 API 中所有操作（范围查找除外）均能够在对数时间内完成的数据结构。
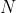个结点的树中，我们希望树高为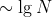，这样我们就能保证所有查找都能在 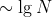次比较内结束，就和二分查找一样（请见命题 B）。不幸的是，在动态插入中保证树的完美平衡的代价太高了。在本节中，我们稍稍放松完美平衡的要求并将学习一种能够保证符号表 API 中所有操作（范围查找除外）均能够在对数时间内完成的数据结构。3.3.1 2-3 查找树
为了保证查找树的平衡性，我们需要一些灵活性，因此在这里我们允许树中的一个结点保存多个键。确切地说，我们将一棵标准的二叉查找树中的结点称为 2- 结点（含有一个键和两条链接），而现在我们引入 3- 结点，它含有两个键和三条链接。2- 结点和 3- 结点中的每条链接都对应着其中保存的键所分割产生的一个区间。
定义。一棵 2-3 查找树或为一棵空树，或由以下结点组成：
2- 结点，含有一个键（及其对应的值）和两条链接，左链接指向的 2-3 树中的键都小于该结点，右链接指向的 2-3 树中的键都大于该结点。
3- 结点，含有两个键（及其对应的值）和三条链接，左链接指向的 2-3 树中的键都小于该结点，中链接指向的 2-3 树中的键都位于该结点的两个键之间，右链接指向的 2-3 树中的键都大于该结点。
和以前一样，我们将指向一棵空树的链接称为空链接。2-3 查找树如图 3.3.1 所示。
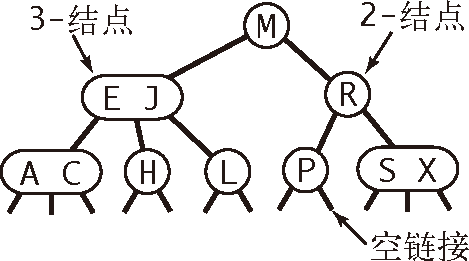
图 3.3.1 2-3 查找树示意图
一棵完美平衡的 2-3 查找树中的所有空链接到根结点的距离都应该是相同的。简洁起见，这里我们用 2-3 树指代一棵完美平衡的 2-3 查找树（在其他情况下这个词应该表示一种更一般的结构）。稍后我们将会学习定义并高效地实现 2- 结点、3- 结点和 2-3 树的基本操作。现在先假设我们已经能够自如地操作它们并来看看应该如何将它们用作查找树。
公开
同步至部落
取消
完成
0/2000
荧光笔
直线
曲线笔记
复制
AI
- 深入了解
- 翻译
- 解释
- 总结
红黑树是一种高效的平衡查找树，通过使用红链接和黑链接来表示2-3树的结构，实现了高效的查找和平衡插入算法。本文详细介绍了红黑树的基本定义和结构，包括红链接和黑链接的特点，以及红黑树与2-3树的对应关系。旋转操作是红黑树中的关键操作，通过图示和描述展示了红黑树的操作过程和如何保持有序性和完美平衡性。性能分析显示红黑树几乎是完美平衡的，查找操作的平均比较次数约为对数级别。红黑树的API实现通过了各种应用的考验，包括许多库实现。总的来说，本文是一份深入了解红黑树的技术参考资料，适合对平衡查找树感兴趣的读者阅读。文章内容详实，通过简洁的语言和图示，读者能够快速了解红黑树的核心概念和操作过程，为进一步深入学习提供了良好的基础。
仅可试看部分内容，如需阅读全部内容，请付费购买文章所属专栏
《算法（第 4 版）》
《算法（第 4 版）》
立即购买
登录 后留言
精选留言
由作者筛选后的优质留言将会公开显示，欢迎踊跃留言。
收起评论