4.3 最小生成树
Robert Sedgewick Kevin Wayne
加权图是一种为每条边关联一个权值或是成本的图模型。这种图能够自然地表示许多应用。在一幅航空图中,边表示航线,权值则可以表示距离或是费用。在一幅电路图中,边表示导线,权值则可能表示导线的长度即成本,或是信号通过这条线路所需的时间。在这些情形中,最令人感兴趣的自然是将成本最小化。在本节中,我们将学习加权无向图模型并用算法回答下面这个问题。
最小生成树。给定一幅加权无向图,找到它的一棵最小生成树。
定义。图的生成树是它的一棵含有其所有顶点的无环连通子图。一幅加权图的最小生成树(MST)是它的一棵权值(树中所有边的权值之和)最小的生成树。(请见图 4.3.1)。
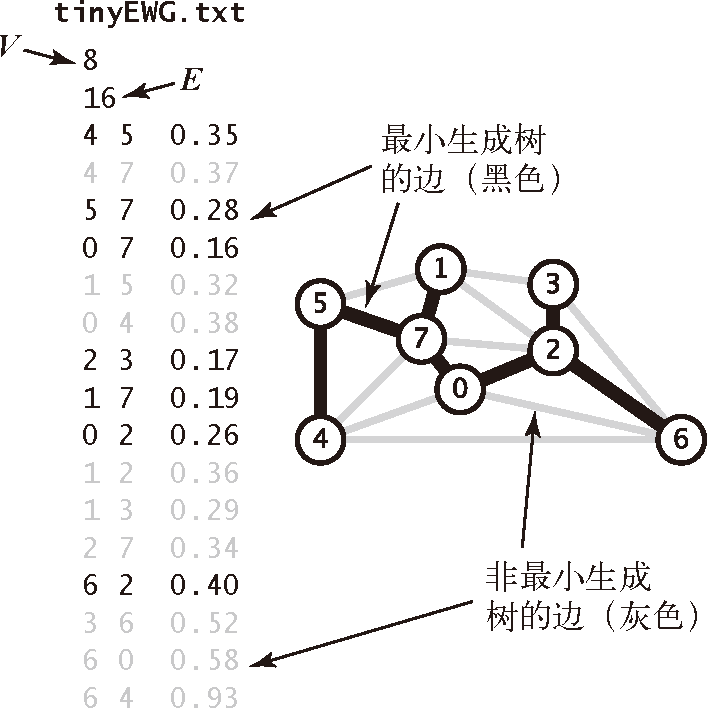
图 4.3.1 一幅加权无向图和它的最小生成树
在本节中,我们会学习计算最小生成树的两种经典算法:Prim 算法和 Kruskal 算法。这些算法理解容易,实现简单。它们是本书中最古老和最知名的算法之一,但它们也根据现代数据结构得到了改进。因为最小生成树的重要应用领域太多,对解决这个问题的算法的研究至少从 20 世纪 20 年代在设计电力分配网络时就开始了。现在,最小生成树算法在设计各种类型的网络(通信、电子、水利、计算机、公路、铁路、航空等)以及自然界中的生物、化学和物理网络等各个领域的研究中都起到了重要的作用,请见表 4.3.1。
表 4.3.1 最小生成树的典型应用
公开
同步至部落
取消
完成
0/2000
笔记
复制
AI
- 深入了解
- 翻译
- 解释
- 总结

本文深入介绍了加权图和最小生成树的概念、应用和相关算法。加权图是一种能够自然地表示许多应用的图模型,而最小生成树则是在给定加权无向图的情况下,寻找其一棵权值最小的生成树。文章详细介绍了最小生成树的典型应用领域,包括电路、航空、电力分配、图像分析等,并回顾了树的基本性质和切分定理。此外,文章还介绍了计算最小生成树的两种经典算法:Prim算法和Kruskal算法,以及贪心算法在解决最小生成树问题中的应用。 文章还介绍了加权无向图的数据类型和相关API,使读者能够快速掌握最小生成树的基本原理和计算方法。整体而言,本文为读者提供了对最小生成树的全面了解,是一篇涵盖理论和实践的高质量技术文章。文章还提供了最小生成树的API和测试用例,以及一些测试数据,帮助读者在实际应用中理解和使用最小生成树算法。 除此之外,文章还介绍了Prim算法的延时实现和即时实现,以及对比了两种实现方式的优劣。通过对算法的具体实现细节进行讲解,读者可以更深入地理解算法的内在原理和实际运行效果。文章通过图示和代码示例的方式生动地展现了算法的执行过程,使读者能够更直观地理解算法的工作机制。 总的来说,本文内容丰富,涵盖了最小生成树的理论基础、应用场景和具体算法实现,对于对图论和算法感兴趣的读者来说,是一篇极具价值的技术文章。文章还提到了一些最小生成树算法的发展趋势和挑战,为读者展示了该领域的前沿动态。
仅可试看部分内容,如需阅读全部内容,请付费购买文章所属专栏
《算法(第 4 版)》
《算法(第 4 版)》
立即购买
登录 后留言
精选留言
由作者筛选后的优质留言将会公开显示,欢迎踊跃留言。
收起评论