2.2 归并排序
Robert Sedgewick Kevin Wayne
在本节中我们所讨论的算法都基于归并这个简单的操作,即将两个有序的数组归并成一个更大的有序数组。很快人们就根据这个操作发明了一种简单的递归排序算法:归并排序。要将一个数组排序,可以先(递归地)将它分成两半分别排序,然后将结果归并起来。你将会看到,归并排序最吸引人的性质是它能够保证将任意长度为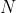 的数组排序所需时间和
的数组排序所需时间和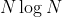 成正比;它的主要缺点则是它所需的额外空间和
成正比;它的主要缺点则是它所需的额外空间和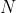 成正比。简单的归并排序如图 2.2.1 所示。
成正比。简单的归并排序如图 2.2.1 所示。
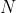 的数组排序所需时间和
的数组排序所需时间和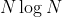 成正比;它的主要缺点则是它所需的额外空间和
成正比;它的主要缺点则是它所需的额外空间和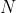 成正比。简单的归并排序如图 2.2.1 所示。
成正比。简单的归并排序如图 2.2.1 所示。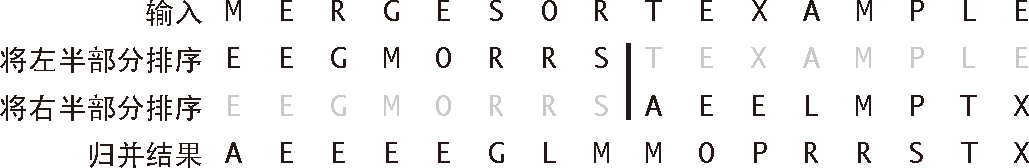
图 2.2.1 归并排序示意图
2.2.1 原地归并的抽象方法
实现归并的一种直截了当的办法是将两个不同的有序数组归并到第三个数组中,两个数组中的元素应该都实现了 Comparable 接口。实现的方法很简单,创建一个适当大小的数组然后将两个输入数组中的元素一个个从小到大放入这个数组中。
但是,当用归并将一个大数组排序时,我们需要进行很多次归并,因此在每次归并时都创建一个新数组来存储排序结果会带来问题。我们更希望有一种能够在原地归并的方法,这样就可以先将前半部分排序,再将后半部分排序,然后在数组中移动元素而不需要使用额外的空间。你可以先停下来想想应该如何实现这一点,乍一看很容易做到,但实际上已有的实现都非常复杂,尤其是和使用额外空间的方法相比。
尽管如此,将原地归并抽象化仍然是有帮助的。与之对应的是我们的方法签名 merge(a, lo, mid, hi),它会将子数组 a[lo..mid] 和 a[mid+1..hi] 归并成一个有序的数组并将结果存放在 a[lo..hi] 中。下面的代码只用几行就实现了这种归并。它将涉及的所有元素复制到一个辅助数组中,再把归并的结果放回原数组中。实现的另一种方法请见练习 2.2.10。
公开
同步至部落
取消
完成
0/2000
笔记
复制
AI
- 深入了解
- 翻译
- 解释
- 总结

归并排序是一种高效的排序算法,能够保证将任意长度为 N 的数组排序所需时间和 NlogN 成正比。该算法的核心思想是将数组分成两半分别排序,然后将结果归并起来。文章介绍了归并排序的原地归并抽象方法,通过将两个有序数组归并到第三个数组中来实现排序。同时,文章还介绍了自顶向下的归并排序算法,通过递归调用将数组分成子数组并进行排序,最后再将有序的子数组归并为最终的排序结果。通过图示和分析展示了归并排序的动态情况和运行时间的分析。此外,文章还提到了对小规模子数组使用插入排序和测试数组是否已经有序等改进方法,以及归并排序的时间复杂度和空间复杂度的讨论。总的来说,归并排序是一种基于分治思想的典型应用,通过对其原理和实现的介绍,读者可以快速了解归并排序的特点和运行原理,从而更好地理解和应用这一排序算法。文章还介绍了自底向上的归并排序算法,以及排序算法的复杂度的讨论,为读者提供了更全面的排序算法知识。文章还讨论了归并排序的最优性和实际应用中的一些局限性,为读者提供了更深入的思考和探讨空间。
仅可试看部分内容,如需阅读全部内容,请付费购买文章所属专栏
《算法(第 4 版)》
《算法(第 4 版)》
立即购买
登录 后留言
精选留言
由作者筛选后的优质留言将会公开显示,欢迎踊跃留言。
收起评论