4.1 无向图
Robert Sedgewick Kevin Wayne
在我们首先要学习的这种图模型中，边（edge）仅仅是两个顶点（vertex）之间的连接。为了和其他图模型相区别，我们将它称为无向图。这是一种最简单的图模型，我们先来看一下它的定义。
定义。图是由一组顶点和一组能够将两个顶点相连的边组成的。
就定义而言，顶点叫什么名字并不重要，但我们需要一个方法来指代这些顶点。一般使用 0 至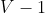
来表示一张含有
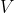个顶点的图中的各个顶点。这样约定是为了方便使用数组的索引来编写能够高效访问各个顶点中信息的代码。用一张符号表来为顶点的名字和 0 到 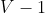的整数值建立一一对应的关系并不困难（请见 4.1.7 节），因此直接使用数组索引作为结点的名称更方便且不失一般性（也不会损失什么效率）。我们用 v-w 的记法来表示连接 v 和 w 的边，w-v 是这条边的另一种表示方法。
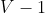来表示一张含有 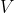个顶点的图中的各个顶点。这样约定是为了方便使用数组的索引来编写能够高效访问各个顶点中信息的代码。用一张符号表来为顶点的名字和 0 到 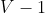的整数值建立一一对应的关系并不困难（请见 4.1.7 节），因此直接使用数组索引作为结点的名称更方便且不失一般性（也不会损失什么效率）。我们用 v-w 的记法来表示连接 v 和 w 的边，w-v 是这条边的另一种表示方法。在绘制一幅图时，用圆圈表示顶点，用连接两个顶点的线段表示边，这样就能直观地看出图的结构。但这种直觉有时也可能会误导我们，因为图的定义和绘出的图像是无关的。例如，图 4.1.1 中的两组图表示的是同一幅图，因为图的构成只有（无序的）顶点和边（顶点对）。
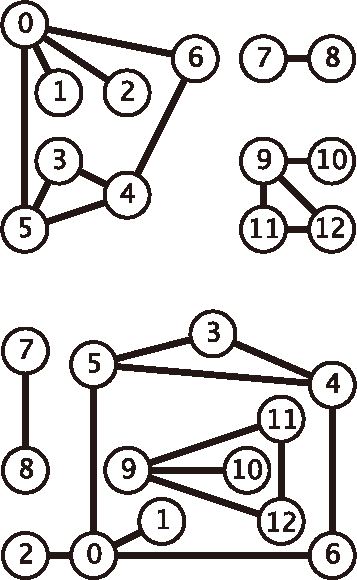
图 4.1.1 同一幅图的两种表示
特殊的图。我们的定义允许出现两种简单而特殊的情况，参见图 4.1.2：
自环，即一条连接一个顶点和其自身的边；
连接同一对顶点的两条边称为平行边。
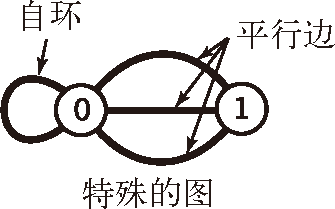
图 4.1.2 特殊的图
数学家常常将含有平行边的图称为多重图，而将没有平行边或自环的图称为简单图。一般来说，实现允许出现自环和平行边（因为它们会在实际应用中出现），但我们不会将它们作为示例。因此，我们用两个顶点就可以指代一条边了。
公开
同步至部落
取消
完成
0/2000
荧光笔
直线
曲线笔记
复制
AI
- 深入了解
- 翻译
- 解释
- 总结
本文深入介绍了无向图的基本概念和相关术语，包括无向图的定义、表示方法，以及与图相关的术语如相邻顶点、度数、子图、路径、环、连通图等。此外，还介绍了无环图、树和生成树的概念，以及树的数学性质。文章还提到了学习寻找生成树和森林的算法，以及这些性质在算法分析和实现中的重要性。另外，文章还介绍了图的密度、稀疏图和稠密图的概念，以及二分图的特点。文章还介绍了图的处理算法的设计模式，以及深度优先搜索和广度优先搜索的概念和实现。通过对迷宫搜索和深度优先搜索的类比，读者可以更直观地理解图的搜索方法。整体而言，本文内容涵盖了无向图的基本概念和相关算法，适合初学者快速了解图论的基本知识。文章还介绍了符号图的概念和相关 API，以及如何使用符号图处理图的测试用例和实现。文章内容丰富，涵盖了图论的基础知识和实际应用，对于对图论感兴趣的读者具有很高的参考价值。
仅可试看部分内容，如需阅读全部内容，请付费购买文章所属专栏
《算法（第 4 版）》
《算法（第 4 版）》
立即购买
登录 后留言
精选留言
由作者筛选后的优质留言将会公开显示，欢迎踊跃留言。
收起评论