练习:后缀数组
Robert Sedgewick Kevin Wayne
6.25 按照图 6.0.15 的样式给出由以下字符串的后缀、后缀的排序、index() 和 lcp() 方法的返回值组成的表格。
a. abacadaba
b. mississippi
c. abcdefghij
d. aaaaaaaaaa
6.26 下面这段代码用于计算字符串的所有后缀,找出其中的问题。
答:它需要平方级别的时间和空间。
6.27 有些应用需要对文本进行回环变位,这个操作会涉及文本中的所有字符。对于 0 到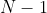 之间的 i,长度为
之间的 i,长度为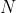 的文本的第 i 次回环变位得到的是它的后
的文本的第 i 次回环变位得到的是它的后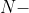 i 个字符和前 i 个字符相连所得的字符串。下面这段代码用于计算文本的所有回环变位,找出其中的问题。
i 个字符和前 i 个字符相连所得的字符串。下面这段代码用于计算文本的所有回环变位,找出其中的问题。
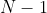 之间的 i,长度为
之间的 i,长度为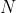 的文本的第 i 次回环变位得到的是它的后
的文本的第 i 次回环变位得到的是它的后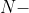 i 个字符和前 i 个字符相连所得的字符串。下面这段代码用于计算文本的所有回环变位,找出其中的问题。
i 个字符和前 i 个字符相连所得的字符串。下面这段代码用于计算文本的所有回环变位,找出其中的问题。 答:它需要平方级别的时间和空间。
6.28 设计一个线性时间的算法来计算给定文本字符串的所有回环变位。
答:
6.29 按照 1.4 节中的假设,给出一个长度为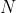 的字符串 SuffixArray 对象对内存的使用情况。
的字符串 SuffixArray 对象对内存的使用情况。
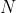 的字符串 SuffixArray 对象对内存的使用情况。
的字符串 SuffixArray 对象对内存的使用情况。6.30 最长公共子字符串。编写一个 SuffixArray 的用例 LCS,接受两个文件名作为命令行参数,读取这两个文本文件并在线性时间内找出同时出现在两个文件中的最长子字符串。(在 1970 年,D.Knuth 猜测这是不可能的。)提示:为字符串 s#t 创建后缀数组,其中 s 和 t 是文本字符串,而 # 是一个两者都不包含的字符)。
6.31 Burrow-Wheeler 变换。Burrow-Wheeler 变换(BWT)是一种用于数据压缩算法中的变换,包括 bzip2 和高吞吐量的基因组测序等。编写一个 SuffixArray 的用例用以下方法在线性时间内计算 BWT。给定一个长度为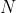 的字符串(以一个文件结束符 $ 结尾,它小于其他任意字符)。使用一个
的字符串(以一个文件结束符 $ 结尾,它小于其他任意字符)。使用一个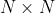 的矩阵,其中每一行均为原文的一个不同的回环变位。按照字典顺序将所有行排序。Burrow-Wheeler 变换就是排序后的矩阵中最右侧的列。例如,mississippi$ 的 BWT 是 ipssm$pissii。Burrow-Wheeler 逆变换(BWI)是 BWT 的逆序。例如,ipssm$pissii 的 BWI 是 mississippi$。编写一个用例,在线性时间内,为某个字符串的 BWT 计算它的 BWI。
的矩阵,其中每一行均为原文的一个不同的回环变位。按照字典顺序将所有行排序。Burrow-Wheeler 变换就是排序后的矩阵中最右侧的列。例如,mississippi$ 的 BWT 是 ipssm$pissii。Burrow-Wheeler 逆变换(BWI)是 BWT 的逆序。例如,ipssm$pissii 的 BWI 是 mississippi$。编写一个用例,在线性时间内,为某个字符串的 BWT 计算它的 BWI。
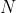 的字符串(以一个文件结束符 $ 结尾,它小于其他任意字符)。使用一个
的字符串(以一个文件结束符 $ 结尾,它小于其他任意字符)。使用一个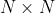 的矩阵,其中每一行均为原文的一个不同的回环变位。按照字典顺序将所有行排序。Burrow-Wheeler 变换就是排序后的矩阵中最右侧的列。例如,mississippi$ 的 BWT 是 ipssm$pissii。Burrow-Wheeler 逆变换(BWI)是 BWT 的逆序。例如,ipssm$pissii 的 BWI 是 mississippi$。编写一个用例,在线性时间内,为某个字符串的 BWT 计算它的 BWI。
的矩阵,其中每一行均为原文的一个不同的回环变位。按照字典顺序将所有行排序。Burrow-Wheeler 变换就是排序后的矩阵中最右侧的列。例如,mississippi$ 的 BWT 是 ipssm$pissii。Burrow-Wheeler 逆变换(BWI)是 BWT 的逆序。例如,ipssm$pissii 的 BWI 是 mississippi$。编写一个用例,在线性时间内,为某个字符串的 BWT 计算它的 BWI。公开
同步至部落
取消
完成
0/2000
笔记
复制
AI
- 深入了解
- 翻译
- 解释
- 总结

本文介绍了后缀数组的相关概念和应用。文章首先介绍了后缀数组的基本概念,包括后缀、后缀的排序、index() 和 lcp() 方法的返回值。接着讨论了计算字符串所有后缀的问题,并指出了其中的问题和解决方法。随后,文章提出了设计一个线性时间算法来计算给定文本字符串的所有回环变位,并给出了相应的解决方案。此外,文章还涉及了最长公共子字符串、Burrow-Wheeler 变换、环形字符串的线性化、重复最长子字符串、较长的重复字符串以及 k-gram 频率统计等相关问题,并给出了相应的解决方法。总的来说,本文涵盖了后缀数组在字符串处理中的多个应用场景,并提供了相应的算法和解决方案。对于对字符串处理感兴趣的读者来说,本文提供了丰富的知识和实用的技术方法,有助于他们更深入地理解和应用后缀数组相关的算法和数据结构。
仅可试看部分内容,如需阅读全部内容,请付费购买文章所属专栏
《算法(第 4 版)》
《算法(第 4 版)》
立即购买
登录 后留言
精选留言
由作者筛选后的优质留言将会公开显示,欢迎踊跃留言。
收起评论