3.4 散列表
Robert Sedgewick Kevin Wayne
如果所有的键都是小整数,我们可以用一个数组来实现无序的符号表,将键作为数组的索引而数组中键 i 处储存的就是它对应的值。这样我们就可以快速访问任意键的值。在本节中我们将要学习散列表。它是这种简易方法的扩展并能够处理更加复杂的类型的键。我们需要用算术操作将键转化为数组的索引来访问数组中的键值对。
使用散列的查找算法分为两步。第一步是用散列函数将被查找的键转化为数组的一个索引。理想情况下,不同的键都能转化为不同的索引值。当然,这只是理想情况,所以我们需要面对两个或者多个键都会散列到相同的索引值的情况。因此,散列查找的第二步就是一个处理碰撞冲突的过程,如图 3.4.1 所示。在描述了多种散列函数的计算后,我们会学习两种解决碰撞的方法:拉链法和线性探测法。
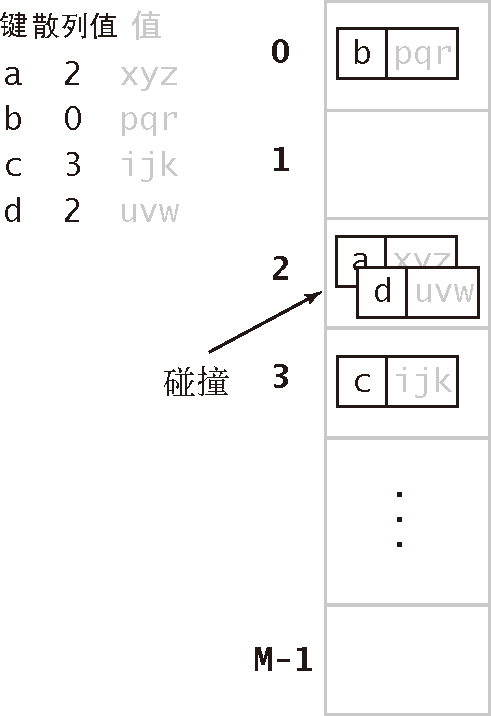
图 3.4.1 散列表的核心问题
散列表是算法在时间和空间上作出权衡的经典例子。如果没有内存限制,我们可以直接将键作为(可能是一个超大的)数组的索引,那么所有查找操作只需要访问内存一次即可完成。但这种理想情况不会经常出现,因为当键很多时需要的内存太大。另一方面,如果没有时间限制,我们可以使用无序数组并进行顺序查找,这样就只需要很少的内存。而散列表则使用了适度的空间和时间并在这两个极端之间找到了一种平衡。事实上,我们不必重写代码,只需要调整散列算法的参数就可以在空间和时间之间作出取舍。我们会使用概率论的经典结论来帮助我们选择适当的参数。
公开
同步至部落
取消
完成
0/2000
笔记
复制
AI
- 深入了解
- 翻译
- 解释
- 总结

本文深入介绍了散列表的基本原理和实际应用,包括散列函数的计算和处理碰撞冲突的方法。文章还详细讨论了不同类型键的散列函数的实现方法,强调了散列表在时间和空间上的权衡,以及如何根据应用需求调整散列算法的参数来取舍时间和空间。此外,还介绍了Java中的散列函数的约定和自定义的hashCode()方法。散列表在一般应用中具有常数级别的查找和插入操作,因此在实现简单符号表时是最佳选择之一。文章还对散列表的性能进行了数学分析,强调了散列表在实际应用中的高性能表现。文章还介绍了散列表动态调整数组大小的方法,以及均摊分析的相关内容。整体而言,本文通过简洁清晰的语言,深入浅出地介绍了散列表的原理和实际应用,适合读者快速了解散列表的概况。
仅可试看部分内容,如需阅读全部内容,请付费购买文章所属专栏
《算法(第 4 版)》
《算法(第 4 版)》
立即购买
登录 后留言
精选留言
由作者筛选后的优质留言将会公开显示,欢迎踊跃留言。
收起评论