10｜搜索算法： 一起来写一个简单的爬虫？
黄清昊
该思维导图由 AI 生成，仅供参考
你好，我是微扰君。
你玩过井字棋的游戏吗？在一个九宫格中，双方轮流用 X 和 O 占领一个格子，某一方的 O 或者 X 三个连成一线时即可获胜。
这样一个简单井字棋的游戏，如果要让你自己写代码实现一个 AI，你会怎么做呢？怎么把博弈过程清晰地表示出来呢？
实际上，许多博弈类游戏的过程，我们都可以用树来表示。根节点就是棋盘为空的状态，终点就是各个棋下完的状态，这样的树也被称为博弈树。下图是井字棋某个局面 3 步内的树状展示：
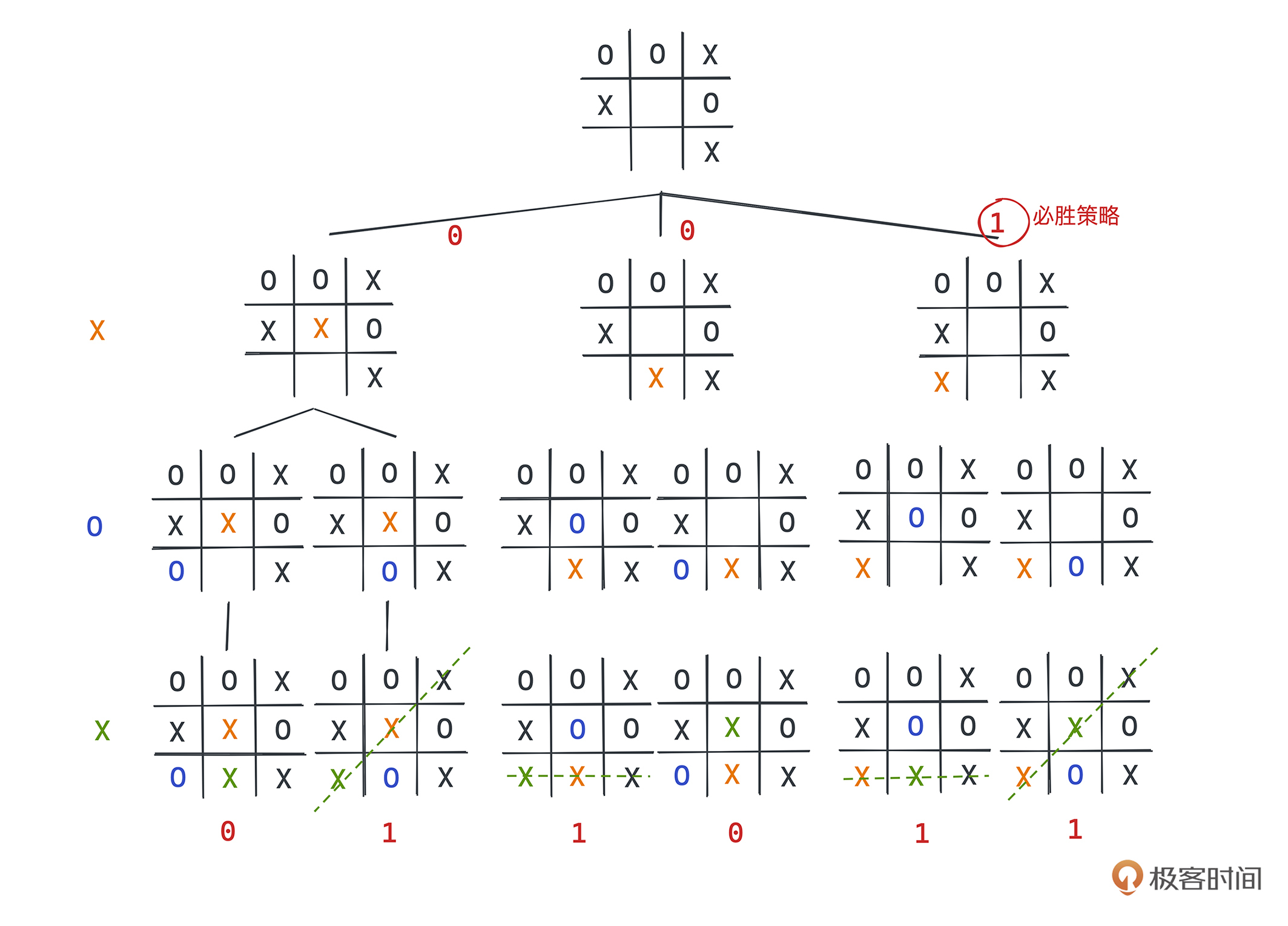
一般来说，对弈双方在做的事情，其实就是找到这棵树上对于自己最优的一种落子方式，使得之后的每条路径，自己都有必胜或者必不败的策略。如果你想要找出一个 AI 策略，最暴力的方式就是直接遍历每一种情况，找到最优的下法，这就是一个典型的搜索问题了。
事实上，这类博弈的游戏要么是先手必不败，要么是后手必不败，所以对全空间的搜索一定是可以写出一个无敌 AI 的，对证明感兴趣的同学可以去搜索“策梅洛定理”了解。
如果暴力遍历，有多少种情况呢？相信你也发现了，就是这么一个简单的井字棋小游戏，终局的数量非常多，达到了 255168 种。我们可以这样来简单地估计它，第一步有 9 种下法，第二步有 8 种下法，显然通过排列组合的知识，占满棋盘一共有 9！=362880 种下法，当然还需要去掉一些中间获胜不应该继续进行对弈的情况。
公开
同步至部落
取消
完成
0/2000
荧光笔
直线
曲线笔记
复制
AI
- 深入了解
- 翻译
- 解释
- 总结
搜索算法在爬虫编写中的应用是本文的重点。文章详细介绍了广度优先搜索算法（BFS）和深度优先搜索算法（DFS）在爬虫领域的实现思路和适用性，并以井字棋游戏和豆瓣用户关系为例进行了生动阐述。通过简单易懂的例子，阐述了BFS和DFS的实现思路和时空复杂度分析，并提供了Python代码示例。总的来说，本文深入浅出地阐述了搜索算法在爬虫编写中的应用，为读者提供了宝贵的技术指导和实践经验。
仅可试看部分内容，如需阅读全部内容，请付费购买文章所属专栏
《业务开发算法 50 讲》，新⼈⾸单¥59
《业务开发算法 50 讲》，新⼈⾸单¥59
立即购买
© 版权归极客邦科技所有，未经许可不得传播售卖。 页面已增加防盗追踪，如有侵权极客邦将依法追究其法律责任。
登录 后留言
全部留言(3)
- 最新
- 精选
第一装甲集群司令克莱斯特2022，勉励自己！编辑回复: 哈哈加油，希望能在留言区经常看到你
2022-01-032
qinsi2. 力扣126 3. 力扣794作者回复: 那可以抓紧补一下题目哦
2022-01-012
Daneil老师新年快乐！作者回复: 新年快乐！ 可以+v: constant_variation 一起跨年学习～
2022-01-01
收起评论
