01 | 线性结构检索：从数组和链表的原理初窥检索本质
该思维导图由 AI 生成，仅供参考
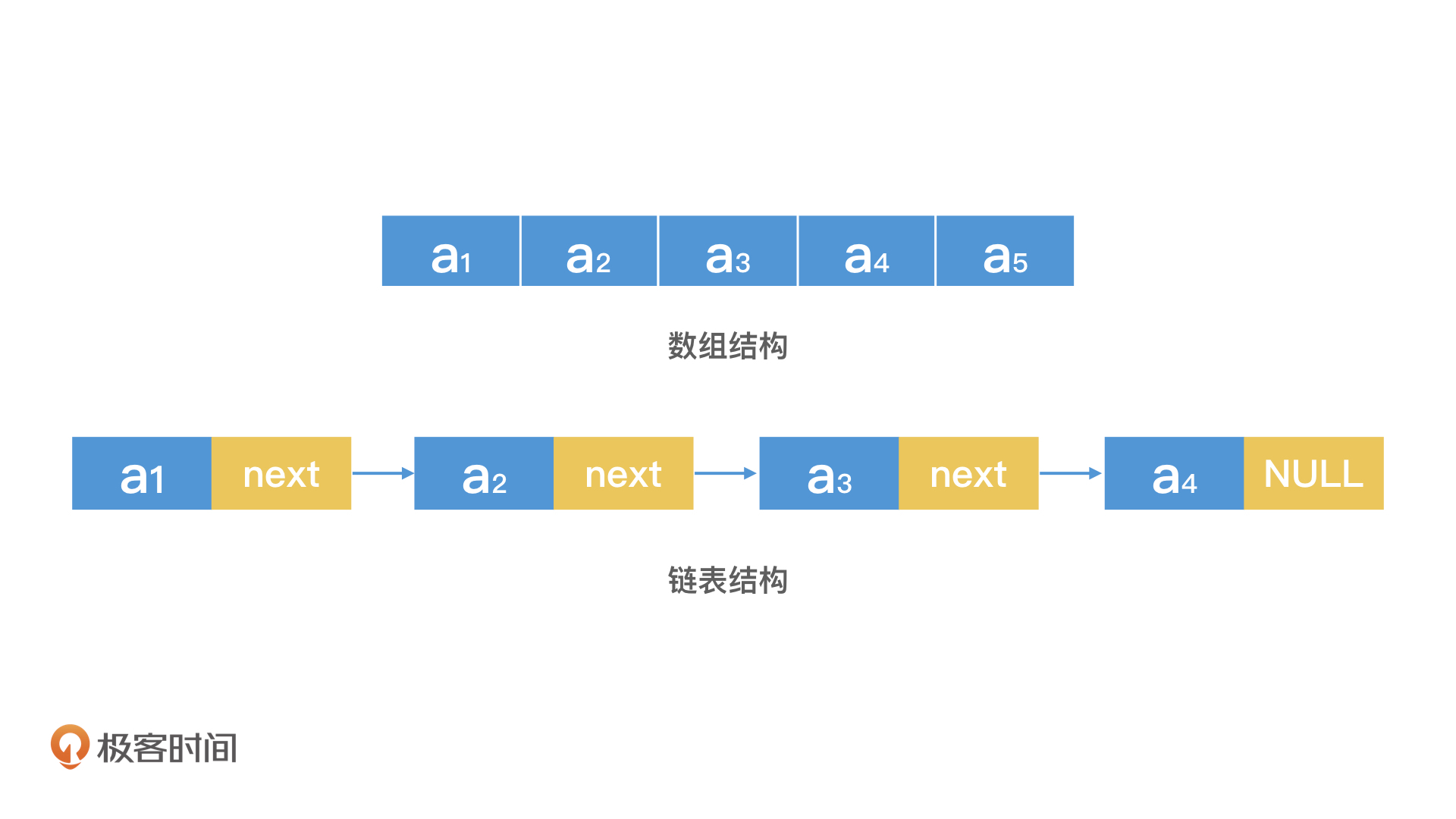
数组和链表有哪些存储特点？
荧光笔
直线
曲线- 深入了解
- 翻译
- 解释
- 总结
数组和链表是常见的线性数据结构，它们的存储特点对检索效率有着重要影响。数组以连续内存空间存储数据，而链表则可以申请不连续的空间，通过指针串联成一条链。对于无序存储的数据，无论是数组还是链表，遍历查找的时间复杂度都是O(n)。然而，对于有序数组，可以通过二分查找算法实现O(log n)的高效检索。相比之下，链表由于缺乏随机访问的特性，检索能力较弱，但在动态调整上更为灵活，能以O(1)的时间代价完成节点的插入和删除。通过灵活改造链表，如将每个节点存储一个小的有序数组，可以提升检索效率，兼顾数组和链表的特点，实现O(log n)的时间代价。因此，合理组织数据的存储方式和灵活应用各种数据结构的特点，是提高检索效率的关键。文章通过深入探讨数组和链表的存储特点以及二分查找算法，为读者提供了对数据结构和检索技术的初步了解，为后续学习和应用提供了基础。文章内容简洁明了，强调了合理组织数据和灵活应用数据结构特点的重要性，为读者提供了对数据结构和检索技术的初步了解，为后续学习和应用提供了基础。
《检索技术核心 20 讲》，新⼈⾸单¥59
全部留言(35)
- 最新
- 精选
无形第二个 第一步二分确定边界，第二步遍历区间值作者回复: 对的。这样的时间代价就是log（n）+（y－x）。这是很常用的方案。许多系统就是这样实现的。 其实还有其他的可行方案，比如两次二分，那么就是log（n）+log（n）； 再比如说，在第一次二分找到x以后，然后在x和数组尾之间再二分找到y。
2020-03-28320- TIGEREI按概率算，二分肯定所需信息量最小阿，log1/2+log1/2小于log0.4+log0.6
作者回复: 用信息论的知识来分析很棒！不过如果是46分的话，出现在6那边的概率是高的，信息量就变小了。可以类比抛硬币，如果硬币出现一面的概率很高，甚至总是出现正面，那么抛硬币的信息量就很小甚至为0。 不过，对于不熟悉信息论的小伙伴也不用担心，该专栏所有的内容都会以直观能理解的语言进行讲解。不会使用大量公式或理论，做到深入浅出，可以放心学习。
2020-03-23316 
嚴脂红.*1、 二分查找是你在不了解数据分布时的最佳策略，37和46都有靠运气假设的成分 2、 可以先二分从min和max之间找出x,然后再二分从x和max之间找出y，中间的元素就是区间内的作者回复: 很棒！ 第一个问题本质就是概率问题。在不知道分布的情况下不能赌运气。 第二个问题，你的第二次二分，是从x到max之间去进行二分。这样和完全在整个数组上进行二分相比，查询空间又少了一些，性能会更好。
2020-03-2715
每天晒白牙1.二分查找概率均匀 2.分别用二分查找 x 和 y 对应的下标，然后取中间的数据作者回复: 简明扼要👍
2020-03-2429
与你一起学算法对于第二题，有点疑惑想问下老师，对于正常的情况(x<=y)，我想到的可以有两种方法去实现，第一种方法是先二分查找x,然后二分查找y,x和y之间的元素就是答案了。第二种方法就是只二分查找x或者y，然后去顺序遍历，和另一个去比较。但是我觉得这两种方法对于不同x和y效率应该是不一样的，有些情况第一种方法较快，有些情况第二种方法较快，想问下老师工业界中的产品(redis)是如何实现区间查询的呢？编辑回复: 非常好！你很好地实践了导读中的学习方法:“多问为什么，多对比不同的方法寻找优缺点”。 1.对于数组怎么范围的问题: 对x和y分别做两次二分查找，时间代价为log（n）+log（n）。 而对x做二分查找，再遍历到y，时间代价为log（n）+（y－x）。 发现没有，我们完全可以根据log（n）和（y－x）的大小进行预判，哪个更快就选哪个！ 当然，除非y－x非常小，否则一般情况下log（n）会更小。 2.对于Redis是怎么实现的问题: 在下一课中，你会学习到，Redis是使用跳表实现的。而跳表是“非连续存储空间”。因此，它不能像数组一样，直接将x到y之间的元素快速复制出来到结果集合中，因此，它只能通过遍历的方式将范围查找的结果写入结果集合中。
2020-03-2347
吴小智讲链表不能快速访问元素，导致二分查找效率更加地下的时候，以为老师会引出快表这种数据结构...觉得说一下快表，文章会更完整一点。作者回复: 你提到了快表，这一点很赞。其实我这一篇里举的将数组和链表灵活结合的例子，就是借鉴了快表的思想。大家有兴趣的话，可以去看看Redis里快表的实现。 我文章中之所以没有明确提出来，是因为作为开篇，我希望能让大家从数组和链表的核心本质去思考问题，而不是去关注“这个新的数据结构好高级好cool”，希望这样对大家的学习和成长能起到一定的帮助。
2020-04-1446
峰因为数组分布未知，所以均匀分布概率最大，也因此二分最优概率最大。如果能够针对有序数组进行分布估计，从而决定每次的最优划分。作者回复: 你说得很正确！我在文中也强调了，“在缺乏分布信息的情况下”，那么二分是效率最优的。 补充一个小知识: 如果有了分布信息，比如说，数据是均匀分布的，最小的数是1，最大的数是1000，那么当我们想查询5的时候，我们第一次查询的位置就不是数组中间了，而是在数组前5/1000的位置进行查找。这种基于均匀分布假设的查找方式，叫做“插值查找”。
2020-03-2424
阿郑看评论也能学到不少，精彩！作者回复: 有些评论还是很有趣的，还有的评论会出现新知识点。因此，大家多多交流，更容易碰撞出火花。 ps:其实我的部落状态也会分享一些相关的知识。
2020-03-282
盘胧二分精髓就在于等分了，性能稳定，对的我们思维的是均分。一种方法论要具有泛化能力才能成为方法论。而37或者46等，都没有做到泛得概念。作者回复: 这也是一个有意思的思路，二分均分的这些思想，在生活中无处不在。某种程度来说，它是“最不惹麻烦的分配方式”。在我们的例子中，它就是可以避免“一直在大的一半去查询”这个麻烦。
2020-03-2522
ykkk88请教下老师用的是哪块画图工具呀~作者回复: PPT就可以了
2020-03-252