24 | 动态规划(上):只需四步,搞定动态规划算法设计
胡光

你好,我是胡光,欢迎回来。
上节课呢,我们学习了递推算法的一般求解步骤:先是定义递推状态,然后推导递推公式,最后是程序设计与实现。并且为了顺利完成递推算法,还介绍了在推导递推公式中的重要指导思想“容斥原理”的相关内容。
递推算法解决的主要类型问题之一,就是计数类问题。就像上节课我们提到的,求 n 个月以后的小兔子数量,求拼凑钱币的方法总数,还有更早之前学习的,求前 n 个数字二进制表示中 1 的个数,等等,这些都是计数类问题。
而在递推算法中,还有一类不同于计数类问题,它是求解最优化解的问题的算法,这类算法有一个专有名称,叫做:动态规划。这就是我们今天要学习的,递推算法中的一个子集算法,动态规划算法。
初识:数字三角形问题
想了解什么是动态规划算法,咱们得先从一个叫做“数字三角形”的简单的动态规划问题开始。数字三角形这个问题很简单,这里我给出了一个由数字组成的 6 层三角形,如下图所示:
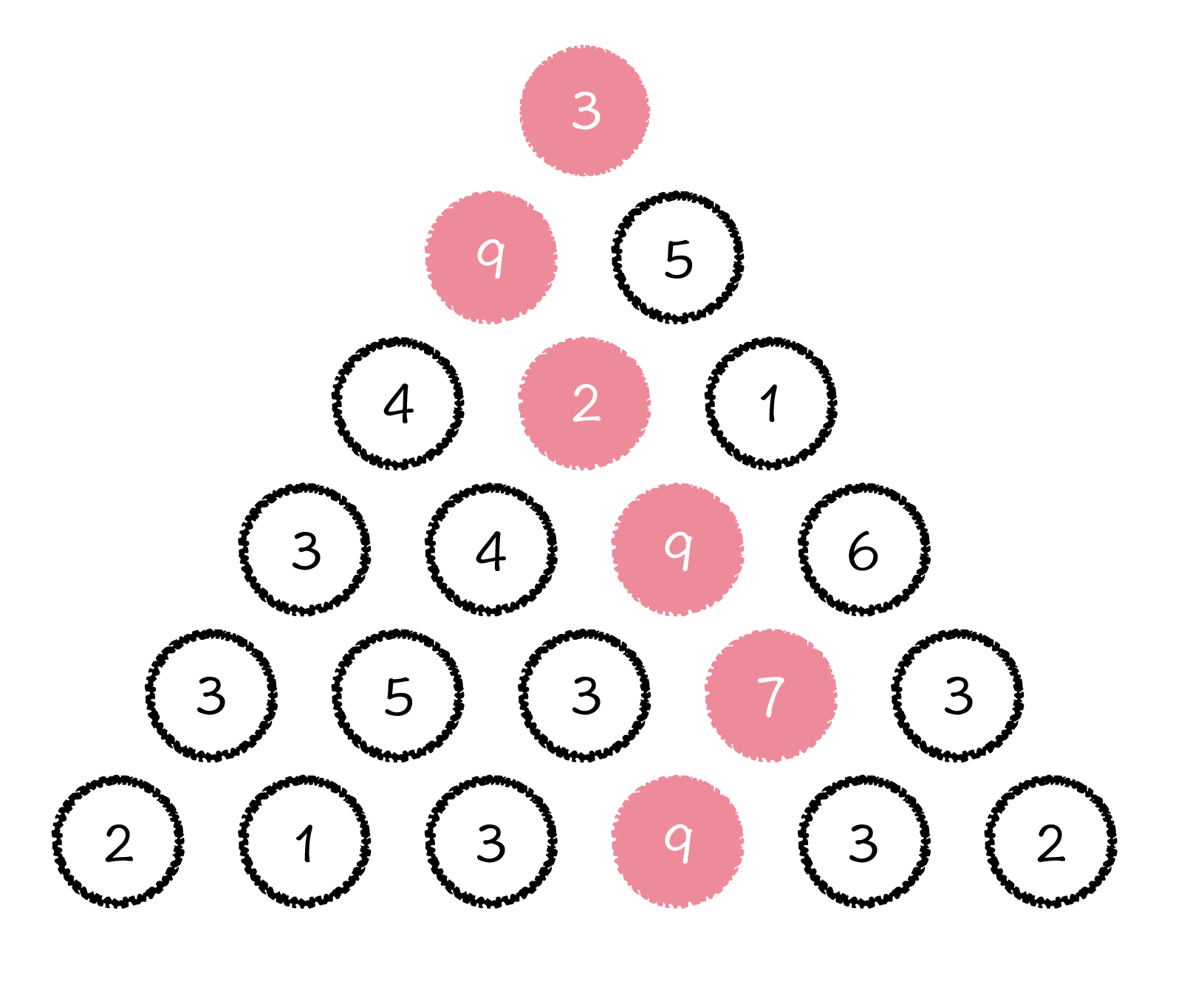
图1: 数字三角形结构示意图
由上到下,第 i 层由 i 个数字组成,目标从第 1 层开始,每次只能向下走到相邻的两个节点,求走到最后一层路径上面数字的最大和值是多少。就像图中标红的一条线路,就是路径和值最大的一条路线,和值为 39。如果给你的是一个 n 层的数字三角形,你该如何解决这个问题呢?
公开
同步至部落
取消
完成
0/2000
笔记
复制
AI
- 深入了解
- 翻译
- 解释
- 总结

动态规划算法是解决最优化问题的一种重要方法。本文通过介绍动态规划算法的设计步骤,从一个简单的数字三角形问题引入动态规划算法的概念。文章提出了动态规划算法的四个步骤:状态定义、状态转移方程、正确性证明以及程序设计与实现。状态定义是解决动态规划问题的关键,不同的状态定义会导致不同的状态转移方程,影响解题难度。文章通过数字三角形问题的两种状态定义展示了不同状态定义对后续求解过程的影响。状态转移方程是根据具体问题和状态定义进行具体分析得出的,并且需要通过数学归纳法证明其正确性。最后,文章强调了动态规划中的状态转移顺序建立在“阶段”概念之上,同时提到了程序设计与实现的重要性。总的来说,本文通过简单易懂的例子和清晰的步骤,帮助读者快速了解动态规划算法的设计方法,强调了状态定义的重要性以及正确性证明的必要性。
仅可试看部分内容,如需阅读全部内容,请付费购买文章所属专栏
《人人都能学会的编程入门课》,新⼈⾸单¥59
《人人都能学会的编程入门课》,新⼈⾸单¥59
立即购买
© 版权归极客邦科技所有,未经许可不得传播售卖。 页面已增加防盗追踪,如有侵权极客邦将依法追究其法律责任。
登录 后留言
全部留言(6)
- 最新
- 精选
 徐洲更嗯嗯 非常认同老师说的 状态定义是DP最关键的一步,前几天做爬楼梯和零钱兑换题目的时候 就发现同一个状态转移方程,调换了内外循环,就导致结果不一样,后来发现是因为当内外循环变了,状态的含义也就变了。我把这个思考过程记录了下来 http://xuzhougeng.top/archives/difference-between-climb-stairs-and-coin-change-ii#more
徐洲更嗯嗯 非常认同老师说的 状态定义是DP最关键的一步,前几天做爬楼梯和零钱兑换题目的时候 就发现同一个状态转移方程,调换了内外循环,就导致结果不一样,后来发现是因为当内外循环变了,状态的含义也就变了。我把这个思考过程记录了下来 http://xuzhougeng.top/archives/difference-between-climb-stairs-and-coin-change-ii#more作者回复: 完美!赞!
2020-03-125 宋不肥#include <stdio.h> int main() { int n, i, j; int s[50][50]; int p[50][50]; scanf("%d", &n); for(i = 1; i <= n; i++) { for(j = 1; j <= i; j++) { scanf("%d", &s[i][j]); } } for(j = 1; j <= n; j++) { p[n][j] = s[n][j]; } for(i = n - 1; i >= 1; i--) { for(j = 1; j <= i; j++) { if(p[i + 1][j] > p[i + 1][j + 1]) { p[i][j] = s[i][j] + p[i + 1][j]; } else { p[i][j] = p[i + 1][j + 1] + s[i][j]; } } } printf("%d\n", p[1][1]); return 0; }
宋不肥#include <stdio.h> int main() { int n, i, j; int s[50][50]; int p[50][50]; scanf("%d", &n); for(i = 1; i <= n; i++) { for(j = 1; j <= i; j++) { scanf("%d", &s[i][j]); } } for(j = 1; j <= n; j++) { p[n][j] = s[n][j]; } for(i = n - 1; i >= 1; i--) { for(j = 1; j <= i; j++) { if(p[i + 1][j] > p[i + 1][j + 1]) { p[i][j] = s[i][j] + p[i + 1][j]; } else { p[i][j] = p[i + 1][j + 1] + s[i][j]; } } } printf("%d\n", p[1][1]); return 0; }作者回复: 不错!
2020-03-151
 罗耀龙@坐忘
罗耀龙@坐忘 茶艺师学编程 第二种状态定义:从下至上 /*三角形 第二种状态定义:从下之上*/ #include <stdio.h> #define MAX(a, b) ((a) > (b) ? (a) : (b)) int c[21] = {3, 9, 5, 4, 2, 1, 3, 4, 9, 6, 3, 5, 3, 7, 3, 2, 1, 3, 9, 3, 2}; int val[7][7] = {0}; int dpval[7][7] = {0}; int tri(int n){ int a = 0; for (int i = 1; i <= n; i++){ for(int j = 1; j <= i; j++){ val[i][j] = c[a++]; } } for (int i = 1; i <= n; i++){ puts("\t"); for(int j = 1; j <= i; j++){ printf("%d ", val[i][j]); } } } int DPF(int n){ if(n == 6){ dpval[n][1] = {2}; dpval[n][2] = {1}; dpval[n][3] = {3}; dpval[n][4] = {9}; dpval[n][5] = {3}; dpval[n][6] = {2}; } for (int i = n; i > 0; i--){ for (int j = 1; j <= i; j++){ dpval[i][j] = MAX(dpval[i + 1][j], dpval[i + 1][j + 1]) + val[i][j]; } } for (int i = 1; i <= n; i++){ puts("\t"); for(int j = 1; j <= i; j++){ printf("%d ", dpval[i][j]); } } } int end( ){ printf("最大值为%d", dpval[1][1]); } int main( ){ puts("原三角:"); tri(6); puts("\n\n(从下之上)处理后的三角;"); DPF(6); puts("\n"); end( ); return 0; }2020-10-201
茶艺师学编程 第二种状态定义:从下至上 /*三角形 第二种状态定义:从下之上*/ #include <stdio.h> #define MAX(a, b) ((a) > (b) ? (a) : (b)) int c[21] = {3, 9, 5, 4, 2, 1, 3, 4, 9, 6, 3, 5, 3, 7, 3, 2, 1, 3, 9, 3, 2}; int val[7][7] = {0}; int dpval[7][7] = {0}; int tri(int n){ int a = 0; for (int i = 1; i <= n; i++){ for(int j = 1; j <= i; j++){ val[i][j] = c[a++]; } } for (int i = 1; i <= n; i++){ puts("\t"); for(int j = 1; j <= i; j++){ printf("%d ", val[i][j]); } } } int DPF(int n){ if(n == 6){ dpval[n][1] = {2}; dpval[n][2] = {1}; dpval[n][3] = {3}; dpval[n][4] = {9}; dpval[n][5] = {3}; dpval[n][6] = {2}; } for (int i = n; i > 0; i--){ for (int j = 1; j <= i; j++){ dpval[i][j] = MAX(dpval[i + 1][j], dpval[i + 1][j + 1]) + val[i][j]; } } for (int i = 1; i <= n; i++){ puts("\t"); for(int j = 1; j <= i; j++){ printf("%d ", dpval[i][j]); } } } int end( ){ printf("最大值为%d", dpval[1][1]); } int main( ){ puts("原三角:"); tri(6); puts("\n\n(从下之上)处理后的三角;"); DPF(6); puts("\n"); end( ); return 0; }2020-10-201
 罗耀龙@坐忘
罗耀龙@坐忘 茶艺师学编程 从上之下 /*三角形 第一种状态定义:从上之下*/ #include <stdio.h> #define MAX(a, b) ((a) > (b) ? (a) : (b)) int c[21] = {3, 9, 5, 4, 2, 1, 3, 4, 9, 6, 3, 5, 3, 7, 3, 2, 1, 3, 9, 3, 2}; int val[7][7] = {0}; int dpval[7][7] = {0}; int tri(int n){ int a = 0; for (int i = 1; i <= n; i++){ for(int j = 1; j <= i; j++){ val[i][j] = c[a++]; } } for (int i = 1; i <= n; i++){ puts("\t"); for(int j = 1; j <= i; j++){ printf("%d ", val[i][j]); } } } int DPF(int n){ if(n == 1){ dpval[n][n] = {3}; } for (int i = 1; i <= n; i++){ for (int j = 1; j <= i; j++){ dpval[i][j] = MAX(dpval[i - 1][j - 1], dpval[i - 1][j]) + val[i][j]; } } for (int i = 1; i <= n; i++){ puts("\t"); for(int j = 1; j <= i; j++){ printf("%d ", dpval[i][j]); } } } int end(int n){ int Mend = 0; for(int i = 1; i <= n; i++){ Mend = MAX(Mend, dpval[n][i]); } printf("最大值为%d", Mend); } int main( ){ puts("原三角:"); tri(6); puts("\n\n(从上之下)处理后的三角;"); DPF(6); puts("\n"); end(6); return 0; }2020-10-201
茶艺师学编程 从上之下 /*三角形 第一种状态定义:从上之下*/ #include <stdio.h> #define MAX(a, b) ((a) > (b) ? (a) : (b)) int c[21] = {3, 9, 5, 4, 2, 1, 3, 4, 9, 6, 3, 5, 3, 7, 3, 2, 1, 3, 9, 3, 2}; int val[7][7] = {0}; int dpval[7][7] = {0}; int tri(int n){ int a = 0; for (int i = 1; i <= n; i++){ for(int j = 1; j <= i; j++){ val[i][j] = c[a++]; } } for (int i = 1; i <= n; i++){ puts("\t"); for(int j = 1; j <= i; j++){ printf("%d ", val[i][j]); } } } int DPF(int n){ if(n == 1){ dpval[n][n] = {3}; } for (int i = 1; i <= n; i++){ for (int j = 1; j <= i; j++){ dpval[i][j] = MAX(dpval[i - 1][j - 1], dpval[i - 1][j]) + val[i][j]; } } for (int i = 1; i <= n; i++){ puts("\t"); for(int j = 1; j <= i; j++){ printf("%d ", dpval[i][j]); } } } int end(int n){ int Mend = 0; for(int i = 1; i <= n; i++){ Mend = MAX(Mend, dpval[n][i]); } printf("最大值为%d", Mend); } int main( ){ puts("原三角:"); tri(6); puts("\n\n(从上之下)处理后的三角;"); DPF(6); puts("\n"); end(6); return 0; }2020-10-201 阿牛学了递推之后 感觉自己的思维都变懒了,写了递推的方法就不知道循环要怎么写了... #include <stdio.h> #define max(a, b) ((a) > (b) ? (a) : (b)) int tgle [7][7] = { {0}, {0, 3}, {0, 9, 5}, {0, 4, 2, 1}, {0, 3, 4, 9, 6}, {0, 3, 5, 3, 7, 3}, {0, 2, 1, 3, 9, 3, 2}, }; // 递推写法 int dp(int i, int j) { if (i == 0) return tgle[i][j]; return max(dp(i - 1, j - 1), dp(i - 1, j)) + tgle[i][j]; } // 循环写法 int s[50][50] = {0}; int dp1(int i, int j) { if (i == 0) return tgle[i][j]; for (int m = 1; m <= i; m++) { for (int n = 1; n <= 10; n++ ) { s[m][n] = max(s[m - 1][n - 1], s[m - 1][n]) + tgle[m][n]; } } return s[i][j]; } int main() { printf("%d\n", tgle[0][4]); printf("%d, %d\n", dp(2, 2), dp1(2, 2)); return 0; }2022-06-19
阿牛学了递推之后 感觉自己的思维都变懒了,写了递推的方法就不知道循环要怎么写了... #include <stdio.h> #define max(a, b) ((a) > (b) ? (a) : (b)) int tgle [7][7] = { {0}, {0, 3}, {0, 9, 5}, {0, 4, 2, 1}, {0, 3, 4, 9, 6}, {0, 3, 5, 3, 7, 3}, {0, 2, 1, 3, 9, 3, 2}, }; // 递推写法 int dp(int i, int j) { if (i == 0) return tgle[i][j]; return max(dp(i - 1, j - 1), dp(i - 1, j)) + tgle[i][j]; } // 循环写法 int s[50][50] = {0}; int dp1(int i, int j) { if (i == 0) return tgle[i][j]; for (int m = 1; m <= i; m++) { for (int n = 1; n <= 10; n++ ) { s[m][n] = max(s[m - 1][n - 1], s[m - 1][n]) + tgle[m][n]; } } return s[i][j]; } int main() { printf("%d\n", tgle[0][4]); printf("%d, %d\n", dp(2, 2), dp1(2, 2)); return 0; }2022-06-19
 罗耀龙@坐忘
罗耀龙@坐忘 茶艺师学编程 两种不一样的状态定义,带来的不仅仅是编写上的不一样,还有的是面对变化的反应难度也不一样。 具体说就是,如果使用第1种从上至下的状态定义,说使用的代码量是比第2种多一点,但是如果这个三角形再增加第7层、第8层,只要把新的数字输进去,这个程序能直接算的。 而第2种,它有一种事后对一个事情盖棺定论的爽快感(说难听点就是事后诸葛亮),就代码量上肯定是比第一种少。但是如果这个三角形再增加第7层、第8层,那这程序就得需要做相应的修改。 一个是保有自身的开放性,能以不变应万变;另一个是虽然处理快,但面对变化就得修改自身。2020-10-20
茶艺师学编程 两种不一样的状态定义,带来的不仅仅是编写上的不一样,还有的是面对变化的反应难度也不一样。 具体说就是,如果使用第1种从上至下的状态定义,说使用的代码量是比第2种多一点,但是如果这个三角形再增加第7层、第8层,只要把新的数字输进去,这个程序能直接算的。 而第2种,它有一种事后对一个事情盖棺定论的爽快感(说难听点就是事后诸葛亮),就代码量上肯定是比第一种少。但是如果这个三角形再增加第7层、第8层,那这程序就得需要做相应的修改。 一个是保有自身的开放性,能以不变应万变;另一个是虽然处理快,但面对变化就得修改自身。2020-10-20
收起评论

