22 | 栈与单调栈:最大矩形面积
胡光

你好,我是胡光,欢迎回来。
上节课我们讲了单调队列这种具有单调性的结构,并且说明了单调队列适合:维护队列处理顺序中的区间最大值,并且我还提到单调队列只是一个铺垫,搞清楚了单调队列的内容,才能更好地学习新的数据结构。
今天我将带你学习一种队列和单调队列的兄弟数据结构,它的性质也很有趣,就是:栈与单调栈。学习这个数据结构的时候呢,我还是要再次强调一下那句话:数据结构,就是定义一种性质,并且维护这种性质。
今日任务
在正式开始学习之前呢,先来看一下今天这 10 分钟的任务吧。
假设有一面木板墙,每块木板的宽度都是 1,你现在想在木板墙上,沿着平行于地面的方向,切割出一块矩形区域。问题来了,如果给出了每一块木板的高度,那么如何切出面积最大的矩形区域?矩形木板墙如下图所示:
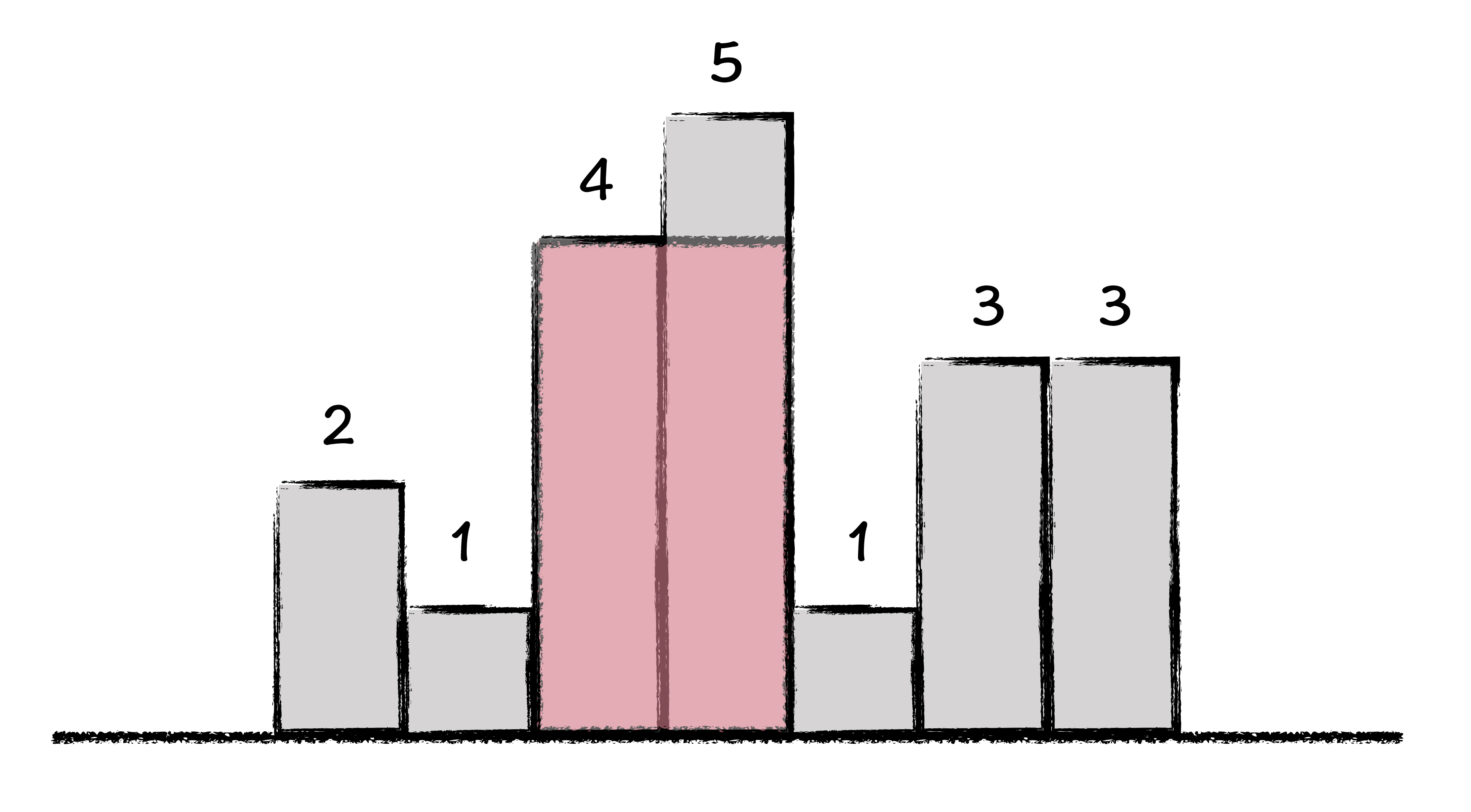
图1: 木板墙示意图
如你所见,图中有 7 块木板,每块木板的高度分别为:2、1、4、5、1、3、3。经过尝试,我们发现最大矩形就是红色阴影部分所示,也就是切割了高度为 4 和 5 两块木板,形成了一个高度为 4,宽度为 2 的矩形区域,这个最大面积为 8。
显而易见的结论:就是切下来的最大的矩形,一定是以最大矩形所在区域最短那块木板作为其高度值。如果不是这样的话,我们就可以提升一点点高度,让切下来的部分更大一点儿。
公开
同步至部落
取消
完成
0/2000
笔记
复制
AI
- 深入了解
- 翻译
- 解释
- 总结

栈与单调栈:最大矩形面积 本文介绍了栈和单调栈的概念及其应用。首先,作者通过生动的比喻和实例解释了栈的基本概念,强调了其后进先出的特性。随后,引入了单调栈的概念,并通过对比单调队列,阐述了单调栈维护最近大于或小于关系的结构。作者还展示了单调栈在解决问题中的应用,如在给定木板高度的情况下,切割出最大矩形面积。特别强调了单调栈的高效性,将时间复杂度从$O(n^2)$降低到$O(n)$,并鼓励读者掌握这一数据结构。最后,作者给出了示例代码,并总结了单调栈的关键知识点。整体而言,本文深入浅出地介绍了栈和单调栈的概念及应用,对于想要深入了解数据结构的读者来说,是一篇值得阅读的文章。
仅可试看部分内容,如需阅读全部内容,请付费购买文章所属专栏
《人人都能学会的编程入门课》,新⼈⾸单¥59
《人人都能学会的编程入门课》,新⼈⾸单¥59
立即购买
© 版权归极客邦科技所有,未经许可不得传播售卖。 页面已增加防盗追踪,如有侵权极客邦将依法追究其法律责任。
登录 后留言
全部留言(8)
- 最新
- 精选
 宋不肥作业打卡: #define MAX 1000 char stack[MAX]; int top = 0; int f(char* s){ if( s == NULL ) return false; for( int i=0; s[i]!='\0'; i++) { if(s[i]=='(' || s[i]=='[' || s[i]=='{') stack[++top] = s[i]; else if( (s[i]==')'&&stack[top]=='(') || (s[i]==']'&&stack[top]=='[') || (s[i]=='}'&&stack[top]=='{') ) top--; else return -1; } if( top == 0 ) return 0; return -1; } 其实上一节和这一节都是用到了两个数组,分别处理值和对应的输入数据的下标,相当于维护了一个单调性的函数映射。而且还是一个分区间的分段函数,其实想通了这个示例代码就很好看了,数组和链表(指针或引用)是最基础的数据结构,其他数据结构也是通过结构体或类来吧数组和链表进行新的组合,而数组和链表在权衡随机访问和插入的时间复杂度和空间复杂度,对cpu缓存的友好性等适用不同的生产环境。但对同一组数据进行这种多个数组的操作,其实都是在模拟函数了,就和我们平时在实验室做数学推导一个道理了,把变量(数组)做好注释,把公式写出来或者画个图就好理解了。
宋不肥作业打卡: #define MAX 1000 char stack[MAX]; int top = 0; int f(char* s){ if( s == NULL ) return false; for( int i=0; s[i]!='\0'; i++) { if(s[i]=='(' || s[i]=='[' || s[i]=='{') stack[++top] = s[i]; else if( (s[i]==')'&&stack[top]=='(') || (s[i]==']'&&stack[top]=='[') || (s[i]=='}'&&stack[top]=='{') ) top--; else return -1; } if( top == 0 ) return 0; return -1; } 其实上一节和这一节都是用到了两个数组,分别处理值和对应的输入数据的下标,相当于维护了一个单调性的函数映射。而且还是一个分区间的分段函数,其实想通了这个示例代码就很好看了,数组和链表(指针或引用)是最基础的数据结构,其他数据结构也是通过结构体或类来吧数组和链表进行新的组合,而数组和链表在权衡随机访问和插入的时间复杂度和空间复杂度,对cpu缓存的友好性等适用不同的生产环境。但对同一组数据进行这种多个数组的操作,其实都是在模拟函数了,就和我们平时在实验室做数学推导一个道理了,把变量(数组)做好注释,把公式写出来或者画个图就好理解了。作者回复: 不错!你理解的很到位!
2020-03-083 Hunter Liu括号的左半部分是入栈,右半部分是出栈,符合这个规律的就是合法序列,否则就是非法的。
Hunter Liu括号的左半部分是入栈,右半部分是出栈,符合这个规律的就是合法序列,否则就是非法的。作者回复: perfect!
2020-03-11 🤪HappyJoo老师,第二行:#define max(a, b) ((a) > (b) : (a) : (b)) 应该是:#define max(a, b) ((a) > (b) ? (a) : (b)) 老师你快醒醒啊,周六了不用工作了!!
🤪HappyJoo老师,第二行:#define max(a, b) ((a) > (b) : (a) : (b)) 应该是:#define max(a, b) ((a) > (b) ? (a) : (b)) 老师你快醒醒啊,周六了不用工作了!!作者回复: yes,你是对的,另外你太皮了。-_-|||,还我的美梦。
2020-03-07 🤪HappyJooLeetcode 题号:有效的括号--20、柱状图中最大的矩形--84。 好久以前用python做过第一题,现在早忘了哈哈~ 思考: 1,加入数组两端的‘-1’就是传说中的哨兵技巧,加入哨兵可以减少边界条件的判断,简化编程难度(JKSJ-数据结构与算法之美,第7讲)。 2,道理我都懂,单调队列单调栈很好理解,唯一的问题,就是代码看不懂(bonehead! bonehead!)!啊!中间一段时间没看,突然就懂了!!!厉害了! 3,老师,你快醒醒!第6行,应该是 h 吧哈哈!
🤪HappyJooLeetcode 题号:有效的括号--20、柱状图中最大的矩形--84。 好久以前用python做过第一题,现在早忘了哈哈~ 思考: 1,加入数组两端的‘-1’就是传说中的哨兵技巧,加入哨兵可以减少边界条件的判断,简化编程难度(JKSJ-数据结构与算法之美,第7讲)。 2,道理我都懂,单调队列单调栈很好理解,唯一的问题,就是代码看不懂(bonehead! bonehead!)!啊!中间一段时间没看,突然就懂了!!!厉害了! 3,老师,你快醒醒!第6行,应该是 h 吧哈哈!作者回复: 醒了,第6行是 h! 代码的话,只是对于思想的一种直白翻译。弄清操作顺序,再对应到代码即可。
2020-03-07 奕有效括号这个就是 leetcode https://leetcode-cn.com/problems/valid-parentheses/ 这道题,但是没有用到单调栈的性质啊
奕有效括号这个就是 leetcode https://leetcode-cn.com/problems/valid-parentheses/ 这道题,但是没有用到单调栈的性质啊作者回复: 对,不是单调栈的题目。就是一道纯的理解栈性质的题目。
2020-03-072
 罗耀龙@坐忘
罗耀龙@坐忘 茶艺师学编程 课文例子 完整可运行代码: #include <stdio.h> #define MAX_N 1000 #define max(a, b) ((a) > (b) ? (a) : (b)) int s[MAX_N + 5], top; int l[MAX_N + 5], r[MAX_N + 5]; int max_matrix_area (int *h, int n){ h[0] = h[n + 1] = -1; top = -1, s[++top] = 0; for (int i = 1; i <= n; i++){ while (top >= 0 && h[s[top]] >= h[i])--top; l[i] = s[top]; s[++top] = i; } top = -1, s[++top] = n + 1; for (int i = n; i >= 1; i--){ while (top >=0 && h[s[top]] >= h[i])--top; r[i] = s[top]; s[++top] = i; } int ans = 0; for (int i = 1; i <= n; i++){ ans = max(ans, (r[i] - l[i] - 1) * h[i] ); } return ans; } int main(){ int h[7] = {2, 1, 4, 5, 1, 3, 3}; int n = 7; int a; a = max_matrix_area(h, n); printf("最大面积为:%d", a); return 0; }2020-10-121
茶艺师学编程 课文例子 完整可运行代码: #include <stdio.h> #define MAX_N 1000 #define max(a, b) ((a) > (b) ? (a) : (b)) int s[MAX_N + 5], top; int l[MAX_N + 5], r[MAX_N + 5]; int max_matrix_area (int *h, int n){ h[0] = h[n + 1] = -1; top = -1, s[++top] = 0; for (int i = 1; i <= n; i++){ while (top >= 0 && h[s[top]] >= h[i])--top; l[i] = s[top]; s[++top] = i; } top = -1, s[++top] = n + 1; for (int i = n; i >= 1; i--){ while (top >=0 && h[s[top]] >= h[i])--top; r[i] = s[top]; s[++top] = i; } int ans = 0; for (int i = 1; i <= n; i++){ ans = max(ans, (r[i] - l[i] - 1) * h[i] ); } return ans; } int main(){ int h[7] = {2, 1, 4, 5, 1, 3, 3}; int n = 7; int a; a = max_matrix_area(h, n); printf("最大面积为:%d", a); return 0; }2020-10-121
 罗耀龙@坐忘
罗耀龙@坐忘 茶艺师学编程 思考题 我也是想了很久才明白,这样的完全包含的序列,要用单调栈来解决,就像是在玩俄罗斯方块,配对的消失(离开栈),合法的序列在进入这个栈后为“空”,不合法的还是会有东西剩下。 代码如下: #include <stdio.h> #define A (a[i] == '(') #define AA ((a[i-1] == '(' ) && ( a[i] == ')')) #define B (a[i] == '[') #define BB ((a[i-1] == '[' ) && ( a[i] == ']')) #define C (a[i] == '{') #define CC ((a[i-1] == '{' ) && ( a[i] == '}')) char a[500] = {0}; int test(char *a){ int b[1000] = {0}; int top = 0; for (int i = 0; a[i] != '\0' ; i++){ if( A || B || C){ b[++top] = i; if( AA || BB || CC){ top -= 2; } } } return top; } int main(){ puts("please input:"); scanf("%c", &a); int c = 0; c = test(a); if ( c == 0 )puts("该序列是合法的。"); else puts("该序列不合法。"); return 0; }2020-10-13
茶艺师学编程 思考题 我也是想了很久才明白,这样的完全包含的序列,要用单调栈来解决,就像是在玩俄罗斯方块,配对的消失(离开栈),合法的序列在进入这个栈后为“空”,不合法的还是会有东西剩下。 代码如下: #include <stdio.h> #define A (a[i] == '(') #define AA ((a[i-1] == '(' ) && ( a[i] == ')')) #define B (a[i] == '[') #define BB ((a[i-1] == '[' ) && ( a[i] == ']')) #define C (a[i] == '{') #define CC ((a[i-1] == '{' ) && ( a[i] == '}')) char a[500] = {0}; int test(char *a){ int b[1000] = {0}; int top = 0; for (int i = 0; a[i] != '\0' ; i++){ if( A || B || C){ b[++top] = i; if( AA || BB || CC){ top -= 2; } } } return top; } int main(){ puts("please input:"); scanf("%c", &a); int c = 0; c = test(a); if ( c == 0 )puts("该序列是合法的。"); else puts("该序列不合法。"); return 0; }2020-10-13 1043
1043 有入口、有出口,先进先出效率高;有入口,入口即出口,先进后出/后进先出效率高。只有一个口子就不能考虑两边同时进行的状态,解决单向问题如果不能环回流动就只能先进后出或者后进先出。 当然怎么做都会把问题解决,但是就像胡老师刚开始就说的把一个水缸打满,用一桶一桶的提回来和一勺子一勺的盛回来的效率是不一样的。问题小、算法高仅能体现思维水平不同,问题大、用算法解决实际问题的时空复杂度简洁就不是仅仅体现思维水平的问题了,大问题用小问题是堆不出来——多少辆马车加一起也得不到一架火箭,那就是天壤之别了。2020-04-19
有入口、有出口,先进先出效率高;有入口,入口即出口,先进后出/后进先出效率高。只有一个口子就不能考虑两边同时进行的状态,解决单向问题如果不能环回流动就只能先进后出或者后进先出。 当然怎么做都会把问题解决,但是就像胡老师刚开始就说的把一个水缸打满,用一桶一桶的提回来和一勺子一勺的盛回来的效率是不一样的。问题小、算法高仅能体现思维水平不同,问题大、用算法解决实际问题的时空复杂度简洁就不是仅仅体现思维水平的问题了,大问题用小问题是堆不出来——多少辆马车加一起也得不到一架火箭,那就是天壤之别了。2020-04-19
收起评论

